- ผู้เขียน Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- แก้ไขล่าสุด 2025-06-01 06:08.
คณิตศาสตร์เป็นเรื่องยาก ง่ายที่จะลืมแม้กระทั่งแนวคิดพื้นฐานเมื่อคุณพยายามจำหลักการและวิธีการต่างๆ มากมาย ต่อไปนี้คือสองวิธีใหม่ในการลดความซับซ้อนของเศษส่วน
ขั้นตอน
วิธีที่ 1 จาก 4: การใช้ปัจจัยร่วมที่ยิ่งใหญ่ที่สุด

ขั้นตอนที่ 1. เขียนตัวหารและตัวหาร
ตัวประกอบคือตัวเลขที่คุณสามารถคูณเพื่อให้ได้ตัวเลขอื่น ตัวอย่างเช่น 3 และ 4 เป็นตัวประกอบของ 12 เพราะคุณสามารถคูณพวกมันเข้าด้วยกันเพื่อให้ได้ 12 ในการจดตัวประกอบของตัวเลข คุณเพียงแค่เขียนตัวเลขทั้งหมดที่สามารถคูณได้เพื่อให้ได้ตัวเลขนั้นและหารลงตัว โดยปัจจัย
-
เขียนตัวประกอบของตัวเลขจากน้อยไปหามาก โดยไม่ลืมรวมตัวประกอบ 1 ตัวอย่างเช่น วิธีเขียนตัวเศษและตัวส่วนของเศษส่วน 24/32 มีดังนี้
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

ขั้นตอนที่ 2 ค้นหาตัวประกอบร่วมที่ยิ่งใหญ่ที่สุด (GCF) ของตัวเศษและตัวส่วน
GCF เป็นจำนวนที่มากที่สุดที่สามารถหารจำนวนตั้งแต่สองตัวขึ้นไปได้เท่าๆ กัน หลังจากที่คุณเขียนตัวประกอบทั้งหมดของจำนวนแล้ว สิ่งที่คุณต้องทำคือหาจำนวนที่มากที่สุดที่เหมือนกันในรายการตัวประกอบทั้งสอง
-
24: 1, 2, 3, 4, 6,
ขั้นตอนที่ 8, 12, 24.
-
32: 1, 2, 4,
ขั้นตอนที่ 8, 16, 32.
-
GCF ของ 24 และ 32 คือ 8 เพราะ 8 เป็นจำนวนที่ใหญ่ที่สุดที่สามารถหาร 24 และ 32 ได้เท่ากัน

ขั้นตอนที่ 3 หารตัวเศษและเศษส่วนด้วย GCF
ตอนนี้ คุณมี GCF แล้ว สิ่งที่คุณต้องทำคือหารตัวเศษและตัวส่วนด้วยจำนวนนั้น เพื่อทำให้เศษส่วนของคุณอยู่ในรูปที่ง่ายที่สุด นี่คือวิธีการ:
- 24/8 = 3
- 32/8 = 4
- เศษส่วนง่ายคือ 3/4

ขั้นตอนที่ 4 ตรวจสอบงานของคุณ
หากคุณต้องการแน่ใจว่าคุณลดรูปเศษส่วนได้อย่างถูกต้อง คุณเพียงแค่ต้องคูณตัวเศษและตัวส่วนใหม่ด้วย GCF ของเศษส่วนนั้นเพื่อให้ได้เศษส่วนเดิมกลับคืนมา นี่คือวิธีการ:
- 3 * 8 = 24
- 4 * 8 = 32
-
คุณได้กลับสู่รูปแบบเดิมซึ่งก็คือ 24/32
คุณยังสามารถตรวจสอบเศษส่วนเพื่อให้แน่ใจว่าจะไม่ทำให้ง่ายขึ้นอีก เนื่องจาก 3 เป็นจำนวนเฉพาะ จึงหารด้วย 1 และตัวมันเองได้เท่านั้น และสี่หารด้วย 3 ไม่ลงตัว ดังนั้นเศษส่วนจึงไม่สามารถลดรูปลงได้อีก
วิธีที่ 2 จาก 4: หารด้วยตัวเลขขนาดเล็ก

ขั้นตอนที่ 1 เลือกจำนวนเล็กน้อย
ด้วยวิธีนี้ คุณจะต้องเลือกตัวเลขเพียงเล็กน้อย เช่น 2, 3, 4, 5 หรือ 7 เพื่อเริ่มต้น ดูเศษส่วนเพื่อให้แน่ใจว่าแต่ละส่วนหารด้วยจำนวนที่คุณเลือกลงตัว ตัวอย่างเช่น หากคุณมีเศษส่วน 24/108 อย่าเลือก 5 เพราะหารด้วย 5 ไม่ลงตัว อย่างไรก็ตาม หากคุณมีเศษส่วน 25/60 ให้ใช้ 5 เป็นจำนวนที่เหมาะสม
สำหรับเศษส่วน 24/32 นั้น 2 เป็นจำนวนที่ดี เนื่องจากจำนวนทั้งสองเป็นจำนวนคู่ จึงหารด้วย 2 ลงตัว

ขั้นตอนที่ 2 แบ่งตัวเศษและตัวส่วนของเศษส่วนด้วยตัวเลข
เศษส่วนใหม่จะประกอบด้วยตัวเศษและตัวส่วนใหม่ ซึ่งคุณจะได้หลังจากหารส่วนบนและส่วนล่างของเศษส่วน 24/32 ด้วย 2 โดยทำดังนี้
- 24/2 = 12
- 32/2 = 16
- เศษส่วนใหม่ของคุณคือ 12/16
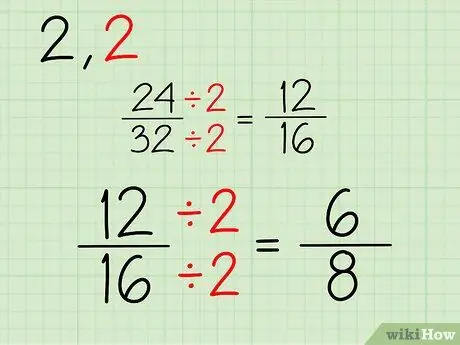
ขั้นตอนที่ 3 ทำซ้ำ
ดำเนินการตามขั้นตอนนี้ต่อไป เนื่องจากตัวเลขทั้งสองเป็นตัวเลขคู่ คุณจึงสามารถหารด้วย 2 ต่อไปได้ หากตัวเศษและตัวส่วนตัวใดตัวหนึ่งหรือทั้งสองตัวเป็นเลขคี่ คุณก็สามารถลองหารด้วยตัวเลขอื่นได้ นี่คือกระบวนการในการทำให้เศษส่วน 12/16 ง่ายขึ้น:
- 12/2 = 6
- 16/2 = 8
- เศษส่วนใหม่ของคุณคือ 6/8

ขั้นตอนที่ 4 ให้หารตัวเลขจนหารไม่ได้อีกต่อไป
ตัวเศษและตัวส่วนใหม่ยังเป็นตัวเลข ดังนั้นคุณสามารถหารด้วย 2 ต่อไปได้ โดยทำดังนี้
- 6/2 = 3
- 8/2 = 4
- เศษส่วนใหม่ของคุณคือ 3/4

ขั้นตอนที่ 5. ตรวจสอบให้แน่ใจว่าไม่สามารถทำให้เศษส่วนง่ายขึ้นได้อีก
ในเศษส่วน 3/4, 3 เป็นจำนวนเฉพาะ ดังนั้นตัวประกอบเป็นเพียง 1 กับตัวมันเอง และ 4 หารด้วย 3 ไม่ลงตัว ดังนั้นเศษส่วนจึงไม่สามารถลดรูปได้อีกต่อไป หากตัวเศษหรือตัวหารของเศษส่วนหารด้วยตัวเลขที่คุณเลือกไม่ได้อีกต่อไป คุณอาจหารด้วยตัวเลขอื่นได้
ตัวอย่างเช่น หากคุณมีเศษส่วน 10/40 และคุณหารตัวเศษและตัวส่วนด้วย 5 ผลลัพธ์จะเป็น 2/8 คุณไม่สามารถหารทั้งตัวเศษและเศษส่วนด้วย 5 ต่อไปได้ แต่คุณสามารถหารทั้งสองด้วย 2 ได้ ดังนั้นผลลัพธ์ที่ได้คือ 1/4

ขั้นตอนที่ 6 ตรวจสอบงานของคุณ
คูณ 3/4 ด้วย 2/2 อีกครั้งสามครั้ง เพื่อให้แน่ใจว่าคุณจะได้เศษส่วนเริ่มต้น ซึ่งก็คือ 24/32 นี่คือวิธีการ:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- สังเกตว่าคุณกำลังหาร 24/32 ด้วย 2 * 2 * 2 ซึ่งเท่ากับหารด้วย 8 ซึ่งเป็น GCF ที่ใหญ่ที่สุดของ 24 และ 32
วิธีที่ 3 จาก 4: การเขียนปัจจัย

ขั้นตอนที่ 1. เขียนเศษส่วนของคุณ
เว้นที่ว่างขนาดใหญ่ทางด้านขวาของกระดาษ - คุณจะต้องใช้พื้นที่นั้นเพื่อจดปัจจัยต่างๆ

ขั้นตอนที่ 2 เขียนตัวประกอบของตัวเศษและส่วน
เพียงอย่างเดียวปัจจัยของทั้งสอง วิธีที่ง่ายที่สุดคือการเขียนปัจจัยต่างๆ ทับกัน เริ่มต้นด้วยหมายเลข 1 และจดปัจจัยต่างๆ
-
ตัวอย่างเช่น ถ้าเศษส่วนของคุณเป็น 24/60 ให้เริ่มต้นด้วย 24
เขียนลงไป: 24 -- 1, 2, 3, 4, 6, 8, 12, 24
-
แล้วเลข 60
จดบันทึก: 60-1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

ขั้นตอนที่ 3 ค้นหาและหารด้วยตัวประกอบร่วมที่ยิ่งใหญ่ที่สุด
คำนี้อาจเขียนเป็น GCF ในหนังสือที่จัดพิมพ์ของคุณ จำนวนใดที่สามารถหารทั้งตัวเศษและส่วนได้มากที่สุด? ตัวเลขอะไรก็ตาม ให้หารทั้งสองตัวเลขด้วยตัวเลขนั้น
ตัวอย่างเช่น จำนวนที่ใหญ่ที่สุดที่เป็นปัจจัยของทั้งสองจำนวนคือ 12 ดังนั้น เราหาร 24 ด้วย 12 และ 60 ด้วย 12 ได้ 2/5 - เศษส่วนอย่างง่ายของเรา
วิธีที่ 4 จาก 4: การใช้ Prime Factor Tree

ขั้นตอนที่ 1 หาตัวประกอบเฉพาะของตัวเศษและตัวส่วน
จำนวนเฉพาะคือจำนวนที่ไม่สามารถหารด้วยจำนวนอื่นใด (นอกจากตัวมันเองและ 1 แน่นอน) 2, 3, 5, 7 และ 11 เป็นตัวอย่างของจำนวนเฉพาะ
- เริ่มต้นด้วยตัวเศษ จาก 24 แบ่งเป็น 2 และ 12 เนื่องจาก 2 เป็นจำนวนเฉพาะอยู่แล้ว คุณจึงไม่ต้องหารมันอีกต่อไป! จากนั้นแบ่ง 12 เป็น 2 ตัวเลข: 2 และ 6 2 เป็นจำนวนเฉพาะ - เยี่ยมมาก! ตอนนี้แบ่ง 6 เป็น 2 ตัวเลข: 2 และ 3 ตอนนี้คุณมี 2, 2, 2 และ 3 เป็นจำนวนเฉพาะของคุณ
- ตอนนี้ทำงานกับตัวส่วน จาก 60 ให้แบ่งต้นไม้ของคุณออกเป็น 2 และ 30 30 จากนั้นหารด้วย 2 และ 15 จากนั้นหาร 15 ออกเป็น 3 และ 5 ซึ่งทั้งสองเป็นจำนวนเฉพาะ ตอนนี้คุณมี 2, 2, 3 และ 5 เป็นจำนวนเฉพาะของคุณ
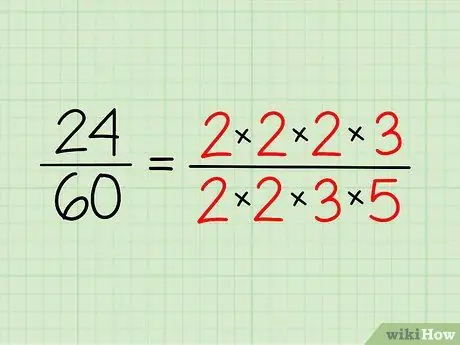
ขั้นตอนที่ 2 เขียนการแยกตัวประกอบเฉพาะของแต่ละตัวเลข
จดจำนวนเฉพาะที่คุณมีสำหรับแต่ละจำนวนแล้วเขียนในรูปแบบการคูณ คุณไม่จำเป็นต้องคูณมัน เพราะเป็นเพียงวิธีทำให้มองเห็นได้ง่ายขึ้น
- ดังนั้นสำหรับ 24 คุณจะได้ 2 x 2 x 2 x 3 = 24
- สำหรับ 60 คุณมี 2 x 2 x 3 x 5 = 60

ขั้นตอนที่ 3 กำจัดปัจจัยเดียวกัน
หมายเลขใด ๆ ที่เป็นส่วนหนึ่งของตัวเลขทั้งสองสามารถทิ้งได้ ในตัวอย่างนี้ ตัวประกอบที่เท่ากันคือคู่ของ 2s และ 3 ลาก่อน!
- ที่เหลือคือ 2 และ 5 - หรือ 2/5! คำตอบเดียวกับที่เราได้รับทางด้านบน
- ถ้าตัวเศษและตัวส่วนเป็นจำนวนคู่ อย่าหารด้วยสองอย่างเดียว ทำการหารต่อไปจนกว่าจำนวนที่คุณได้รับจะไม่สามารถแบ่งได้อีก

