- ผู้เขียน Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- แก้ไขล่าสุด 2025-06-01 06:08.
การลบเป็นเพียงการลบตัวเลขหนึ่งจากอีกจำนวนหนึ่ง การลบจำนวนเต็มหนึ่งจากอีกจำนวนหนึ่งเป็นเรื่องง่าย แต่การลบอาจทำได้ยากหากคุณลบเศษส่วนหรือทศนิยม เมื่อคุณเข้าใจการลบแล้ว คุณจะสามารถใช้แนวคิดทางคณิตศาสตร์ที่ซับซ้อนยิ่งขึ้น และสามารถบวก คูณ และหารตัวเลขได้ง่ายขึ้น
ขั้นตอน
วิธีที่ 1 จาก 6: การลบจำนวนเต็มจำนวนมากโดยการยืม

ขั้นตอนที่ 1 เขียนตัวเลขจำนวนมาก
ตัวอย่างเช่น คุณต้องการแก้ปัญหา 32 - 17 ให้เขียน 32 ก่อน

ขั้นตอนที่ 2 เขียนจำนวนที่น้อยกว่าด้านล่าง
ตรวจสอบให้แน่ใจว่าคุณใส่ค่าหลักสิบและหนึ่งในคอลัมน์ที่ถูกต้อง เพื่อให้ 3 จาก 32 อยู่เหนือ 1 จาก 17 และ 2 ของ 32 อยู่เหนือ 7 ของ 17 โดยตรง
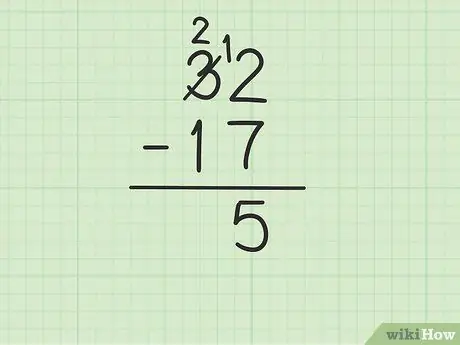
ขั้นตอนที่ 3 ลบตัวเลขบนในคอลัมน์หน่วยจากตัวเลขด้านล่าง
อย่างไรก็ตาม อาจซับซ้อนขึ้นได้หากจำนวนด้านล่างมากกว่าจำนวนด้านบน ในกรณีนี้ 7 มากกว่า 2 นี่คือสิ่งที่คุณต้องทำ:
- คุณต้องยืมจากหมายเลข 3 ของ 32 (เรียกอีกอย่างว่าการจัดกลุ่ม) เพื่อเปลี่ยน 2 เป็น 12
- ข้ามหมายเลข 3 จาก 32 แล้วแทนที่ด้วยหมายเลข 2 ในขณะที่หมายเลข 2 กลายเป็น 12
- ตอนนี้คุณสามารถลบ 12-7 ซึ่งเท่ากับ 5 เขียน 5 ใต้ตัวเลขสองตัวที่คุณกำลังลบเพื่อให้อยู่ในคอลัมน์หน่วยของแถวใหม่
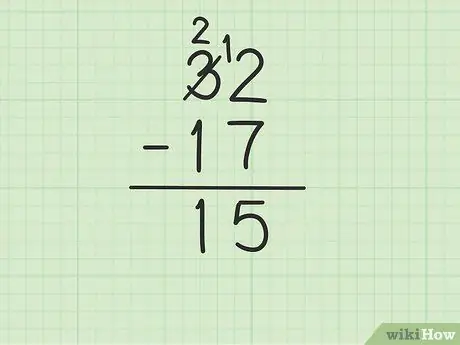
ขั้นที่ 4. ลบเลขบนในหลักสิบจากเลขล่าง
จำไว้ว่า 3 กลายเป็น 2 ตอนนี้ลบ 1 จาก 17 จาก 2 ด้านบนเพื่อให้ได้ (2-1) 1 เขียน 1 ด้านล่างในคอลัมน์หลักสิบทางด้านซ้ายของ 5 ในคอลัมน์หน่วย คุณเขียน 15 นั่นคือ 32 - 17 = 15
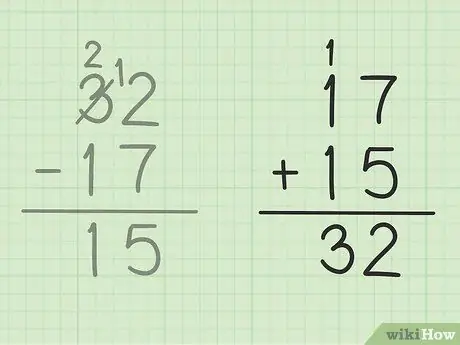
ขั้นตอนที่ 5. ตรวจสอบงานของคุณ
หากคุณต้องการแน่ใจว่าคุณลบตัวเลขสองตัวได้อย่างถูกต้อง สิ่งที่คุณต้องทำคือรวมคำตอบของคุณด้วยตัวเลขที่น้อยกว่าเพื่อให้ได้ตัวเลขมาก ในปัญหานี้ คุณต้องบวกคำตอบของคุณ 15 ให้กับจำนวนการลบที่น้อยกว่า 17. 15 + 17 = 32 เพื่อให้คำตอบของคุณถูกต้อง ปลอดภัย!
วิธีที่ 2 จาก 6: ลบจำนวนเต็มขนาดเล็ก
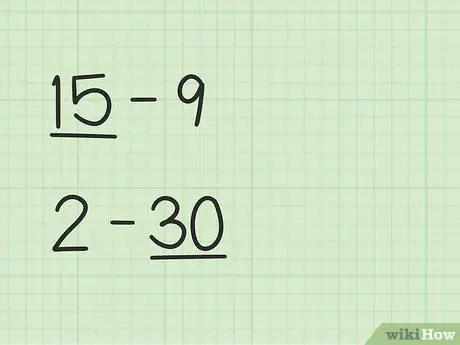
ขั้นตอนที่ 1 ค้นหาจำนวนที่มากกว่า
ปัญหาเช่น 15 -9 จะมีวิธีที่แตกต่างจาก 2 - 30
- ในคำถามที่ 15 - 9 ตัวเลขแรก 15 มากกว่าตัวเลขที่สอง 9
- ในคำถามที่ 2 - 30 ตัวเลขที่สองคือ 30 มากกว่าตัวเลขแรก 2.
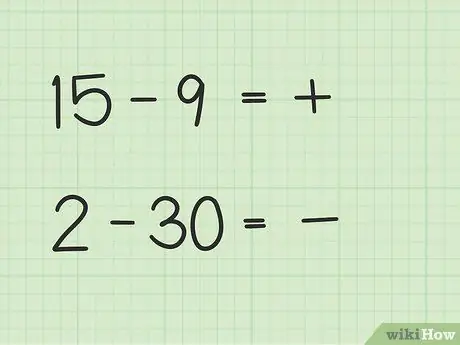
ขั้นตอนที่ 2 ตัดสินใจว่าคำตอบของคุณจะเป็นบวกหรือลบ
หากจำนวนแรกมากกว่า คำตอบจะเป็นบวก หากจำนวนที่สองมากกว่า คำตอบจะเป็นลบ
- ในคำถามแรก 15 - 9 คำตอบของคุณเป็นบวกเพราะตัวเลขแรกมากกว่าตัวเลขที่สอง
- ในคำถามที่สอง 2-30 คำตอบของคุณเป็นค่าลบ เนื่องจากจำนวนที่สองมากกว่าตัวเลขแรก
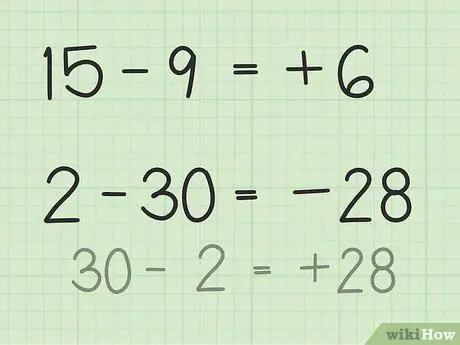
ขั้นตอนที่ 3 ค้นหาความแตกต่างระหว่างตัวเลขสองตัว
ในการลบตัวเลขสองตัว คุณต้องจินตนาการถึงความแตกต่างระหว่างตัวเลขทั้งสองและคำนวณตัวเลขระหว่างตัวเลขทั้งสอง
- สำหรับคำถามที่ 15 - 9 ลองนึกภาพชิปโป๊กเกอร์ 15 กอง ทิ้ง 9 ชิปและ 6 ชิปเท่านั้น ดังนั้น 15 - 9 = 6 คุณสามารถจินตนาการถึงเส้นจำนวนได้ นึกถึงตัวเลขตั้งแต่ 1 ถึง 15 แล้วทิ้งหรือคืน 9 หน่วยเพื่อให้คุณได้ 6
- สำหรับคำถามที่ 2-30 วิธีที่ง่ายที่สุดในการแก้ปัญหานี้คือกลับค่าตัวเลขและทำให้ผลลัพธ์เป็นลบหลังจากลบออก ดังนั้น 30 - 2 = 28 ดังนั้น 28 และ 30 จึงมีความแตกต่างเป็น 2 ทีนี้ ให้ผลลัพธ์เป็นลบ เพราะคุณได้พิจารณาแล้วว่าคำตอบนั้นเป็นลบเพราะจำนวนที่สองมากกว่าตัวเลขแรก ดังนั้น 2 - 30 = -28
วิธีที่ 3 จาก 6: การลบทศนิยม
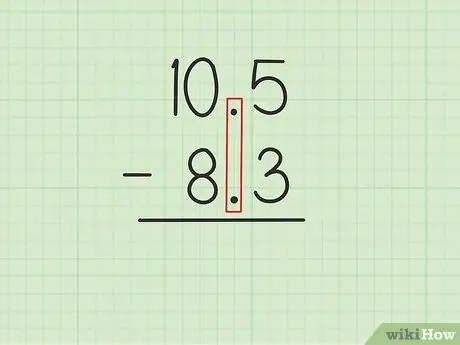
ขั้นตอนที่ 1 เขียนจำนวนที่มากกว่าทับจำนวนที่น้อยกว่าโดยให้จุดทศนิยมอยู่ในแนวเดียวกัน
สมมติว่าคุณต้องการแก้ปัญหาต่อไปนี้: 10, 5 - 8, 3 เขียน 10, 5 ส่วน 8, 3 เพื่อให้จุดทศนิยมของตัวเลขทั้งสองขนานกัน, 5 จาก 10, 5 ต้องอยู่เหนือโดยตรง, 3 จาก 8, 3 และ 0 จาก 10, 5 ต้องอยู่เหนือ 8 จาก 8, 3
หากคุณมีปัญหาเพราะตัวเลขสองตัวหลังจุดทศนิยมไม่เหมือนกัน ให้เขียน 0 ลงในช่องว่างจนกว่าผลรวมของตัวเลขจะเท่ากัน ตัวอย่างเช่น ปัญหาคือ 5, 32 - 4, 2 คุณสามารถเขียนเป็น 5, 32 - 4, 2 0. สิ่งนี้จะไม่เปลี่ยนค่าของตัวเลขที่สอง แต่จะทำให้การลบตัวเลขทั้งสองง่ายขึ้น

ขั้นตอนที่ 2 ลบตัวเลขบนในหลักสิบออกจากตัวเลขด้านล่าง
ในกรณีนี้ คุณต้องลบ 3 จาก 5. 5 - 3 = 2 ดังนั้นคุณต้องเขียน 2 ใต้ 3 ของ 8, 3
ตรวจสอบให้แน่ใจว่าคุณใส่จุดทศนิยมในคำตอบเพื่อให้เขียนเป็น 2

ขั้นตอนที่ 3 ลบตัวเลขที่อยู่เหนือคอลัมน์หน่วยจากตัวเลขด้านล่าง
คุณต้องลบ 8 จาก 0 ยืม 1 จากหลักสิบเพื่อเปลี่ยน 0 เป็น 10 และลบ 10 - 8 เพื่อให้ได้ 2 คุณยังสามารถนับ 10 - 8 โดยไม่ต้องยืมเพราะไม่มีตัวเลขในคอลัมน์หลักสิบที่สอง เขียนคำตอบภายใต้ 8 ทางด้านซ้ายของจุดทศนิยม

ขั้นตอนที่ 4 เขียนผลลัพธ์สุดท้ายของคุณ
ผลลัพธ์สุดท้ายของคุณคือ 2, 2

ขั้นตอนที่ 5. ตรวจสอบงานของคุณ
หากคุณต้องการให้แน่ใจว่าการลบทศนิยมของคุณถูกต้อง สิ่งที่คุณต้องทำคือรวมคำตอบของคุณด้วยตัวเลขที่น้อยกว่าเพื่อให้ได้จำนวนที่มากขึ้น 2, 2 + 8, 3 = 10, 5 คุณทำเสร็จแล้ว
วิธีที่ 4 จาก 6: ลบเศษส่วน

ขั้นตอนที่ 1 จัดตำแหน่งตัวส่วนและตัวเศษของเศษส่วน
สมมติว่าคุณต้องการแก้ปัญหา 13/10 - 3/5 เขียนโจทย์ให้ตัวเศษสองตัว 13 และ 3 และตัวส่วนสองตัว 10 และ 5 อยู่ตรงข้ามกัน ตัวเลขสองตัวนี้คั่นด้วยเครื่องหมายลบ วิธีนี้จะช่วยให้คุณเห็นภาพปัญหาและแก้ไขได้ง่ายขึ้น

ขั้นตอนที่ 2 ค้นหาตัวส่วนร่วมน้อยที่สุด
ตัวส่วนร่วมน้อยที่สุดคือจำนวนที่น้อยที่สุดที่สามารถหารด้วยตัวเลขสองตัว ในตัวอย่างนี้ คุณต้องหาตัวส่วนร่วมที่เล็กที่สุดที่หารด้วย 10 กับ 5 ลงตัว คุณจะพบว่า 10 เป็นตัวส่วนร่วมที่เล็กที่สุดสำหรับตัวเลขทั้งสองเพราะ 10 หารด้วย 10 และ 5 ลงตัว
โปรดทราบว่าตัวส่วนร่วมน้อยที่สุดของตัวเลขสองตัวนั้นไม่ใช่ตัวหารตัวใดตัวหนึ่งเสมอไป ตัวอย่างเช่น ตัวส่วนร่วมที่เล็กที่สุดสำหรับ 3 และ 2 คือ 6 เนื่องจาก 6 เป็นจำนวนที่น้อยที่สุดที่สามารถหารด้วยตัวเลขสองตัวได้
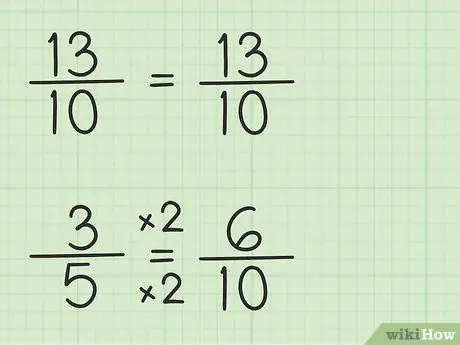
ขั้นตอนที่ 3 เขียนเศษส่วนโดยใช้ตัวส่วนเดียวกัน
เศษส่วน 13/10 สามารถเขียนได้แบบเดียวกันเพราะตัวส่วนคือ 10 ตัวส่วนร่วมที่เล็กที่สุด ซึ่งก็คือ 10 คูณ 1 อย่างไรก็ตาม เศษส่วน 3/5 ต้องเขียนใหม่เพราะตัวส่วนคือ 5 ตัวส่วนร่วมที่เล็กที่สุด ซึ่งก็คือ 10 คูณ 2 ดังนั้นเศษส่วน 3/5 ต้องคูณด้วย 2/2 เพื่อให้ได้ตัวส่วน 10 ดังนั้น 3/5 x 2/2 = 6/10 คุณพบเศษส่วนที่เท่ากัน 3/5 เทียบเท่ากับ 6/10 แม้ว่า 6/10 อนุญาตให้คุณลบตัวเลขแรกได้ 13/10
เขียนคำถามใหม่ดังนี้ 13/10 - 6/10
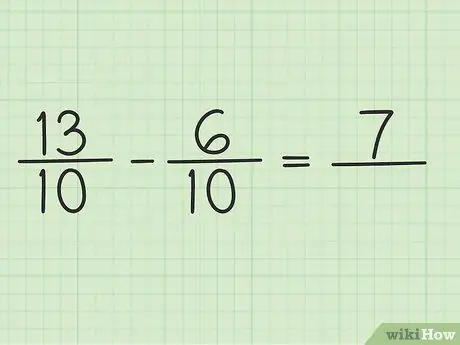
ขั้นตอนที่ 4 ลบตัวเศษเป็นตัวเลขสองตัว
แค่ลบ 13 - 6 ผลลัพธ์ก็คือ 7 คุณไม่สามารถเปลี่ยนตัวส่วนของเศษส่วนได้
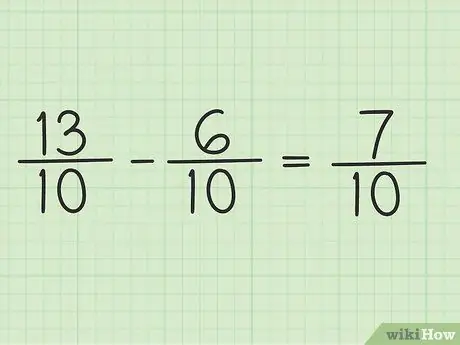
ขั้นตอนที่ 5. เขียนตัวเศษใหม่ทับตัวส่วนเดียวกันเพื่อให้ได้ผลลัพธ์สุดท้าย
ตัวเศษใหม่คือ 7 เศษส่วนทั้งสองตัวมีส่วนเป็น 10 ผลลัพธ์สุดท้ายของคุณคือ 7/10
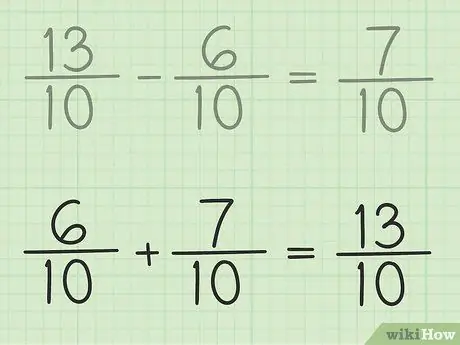
ขั้นตอนที่ 6 ตรวจสอบงานของคุณ
หากคุณต้องการแน่ใจว่าคุณลบเศษส่วนอย่างถูกต้อง ให้บวกคำตอบกับเศษส่วนที่เล็กลงเพื่อให้ผลลัพธ์เป็นเศษส่วนมากขึ้น 7/10 + 6/10 = 13/10. มันเสร็จแล้ว
วิธีที่ 5 จาก 6: การลบเศษส่วนออกจากจำนวนเต็ม

ขั้นตอนที่ 1. เขียนปัญหา
ตัวอย่างเช่น สมมติว่าคุณต้องการแก้ปัญหาต่อไปนี้: 5 -. เขียนมันลง.
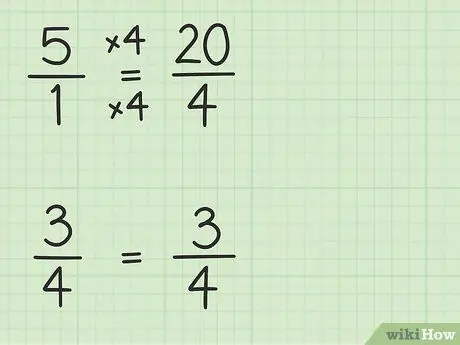
ขั้นตอนที่ 2 แปลงจำนวนเต็มเป็นเศษส่วนที่มีตัวส่วนเหมือนกันกับเศษส่วนอื่นๆ
คุณจะแปลง 5 เป็นเศษส่วนด้วยตัวส่วนเป็น 4 เพื่อให้สามารถลบตัวเลขสองตัวได้ คุณต้องคิด 5 เป็นเศษส่วนของ 5/1. จากนั้น คุณสามารถคูณตัวเศษและตัวส่วนของเศษส่วนใหม่ด้วย 4 เพื่อทำให้ตัวส่วนของตัวเลขทั้งสองเท่ากัน ดังนั้น 5/1 x 4/4 = 20/4 เศษส่วนนี้เท่ากับ 5 แต่ให้คุณลบเลขสองตัวได้
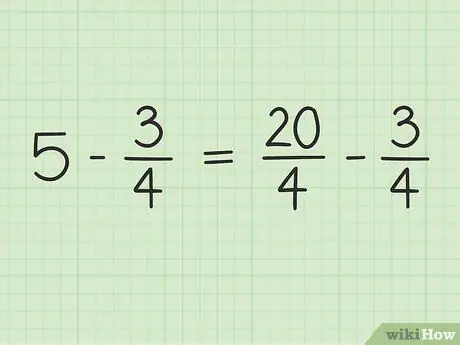
ขั้นตอนที่ 3 เขียนปัญหาใหม่
ปัญหาใหม่สามารถเขียนได้ดังนี้: 20/4 - 3/4
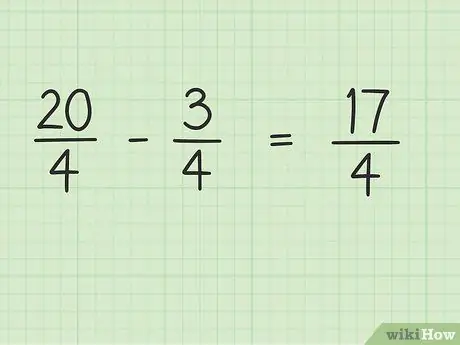
ขั้นตอนที่ 4 ลบตัวเศษของเศษส่วนในขณะที่ตัวส่วนยังคงเหมือนเดิม
ทีนี้ ลบ 20 ด้วย 3 เพื่อให้ได้ผลลัพธ์สุดท้าย 20 - 3 = 17 ดังนั้น 17 เป็นตัวเศษใหม่ คุณสามารถปล่อยให้ตัวส่วนเหมือนกัน
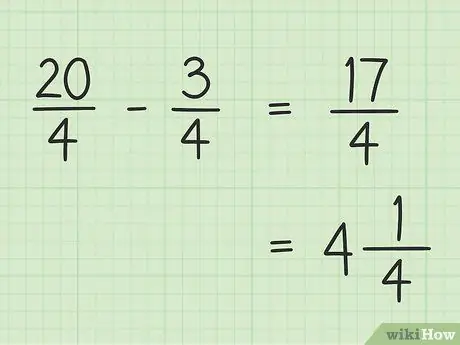
ขั้นตอนที่ 5. เขียนผลลัพธ์สุดท้ายของคุณ
ผลลัพธ์สุดท้ายของคุณคือ 17/4 หากคุณต้องการเขียนเป็นจำนวนคละ ให้หาร 17 ด้วย 4 เพื่อให้ผลลัพธ์เป็น 4 และเศษเหลือเป็น 1 เพื่อให้ 17/4 สุดท้ายของคุณเท่ากับ 4
วิธีที่ 6 จาก 6: การลบตัวแปร
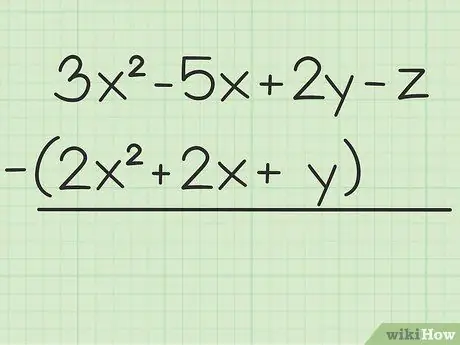
ขั้นตอนที่ 1. เขียนปัญหาที่คุณต้องการแก้ไข
ตัวอย่างเช่นคำถามต่อไปนี้: 3x2 - 5x + 2y - z - (2x2 + 2x + y) เขียนตัวแปรชุดแรกในส่วนที่สอง
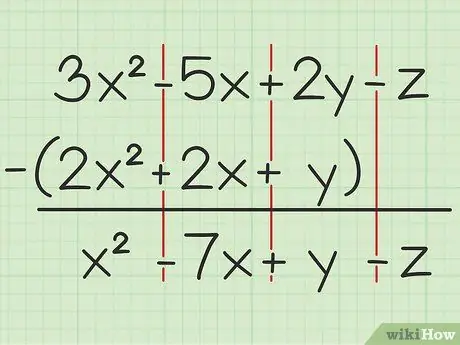
ขั้นตอนที่ 2 ลบตัวแปรเดียวกัน
หากคุณพบตัวแปร คุณสามารถเพิ่มหรือลบตัวแปรเดียวกันได้เท่านั้น และตัวแปรที่เขียนด้วยดีกรีกำลังสองเท่ากัน นั่นหมายความว่าคุณสามารถลบ 4x2 จาก 7x2แต่ไม่สามารถลบ 4x จาก 4y ได้ ดังนั้น คุณสามารถแยกปัญหาออกเป็นดังนี้:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
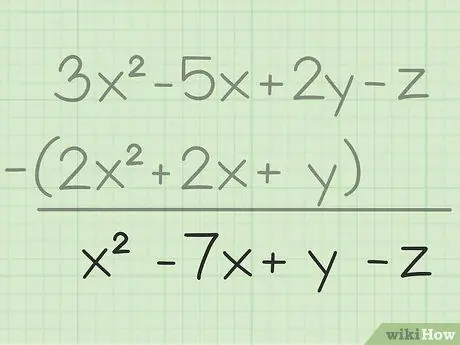
ขั้นตอนที่ 3 เขียนผลลัพธ์สุดท้ายของคุณ
คุณได้ลบตัวแปรเดียวกันทั้งหมดแล้ว สิ่งที่คุณต้องทำคือเขียนผลลัพธ์สุดท้ายของคุณ ซึ่งจะมีตัวแปรทั้งหมดที่คุณลบ นี่คือผลลัพธ์สุดท้าย:

