ส่วนกลับหรือส่วนกลับมีประโยชน์มากในสมการพีชคณิตทุกประเภท ตัวอย่างเช่น เมื่อคุณหารเศษส่วนหนึ่งด้วยอีกเศษหนึ่ง คุณจะคูณเศษส่วนแรกด้วยส่วนกลับของส่วนที่สอง คุณต้องใช้ตัวผกผันเมื่อมองหาสมการของเส้นตรง
ขั้นตอน
วิธีที่ 1 จาก 3: การหาค่าผกผันของเศษส่วนหรือจำนวนเต็ม
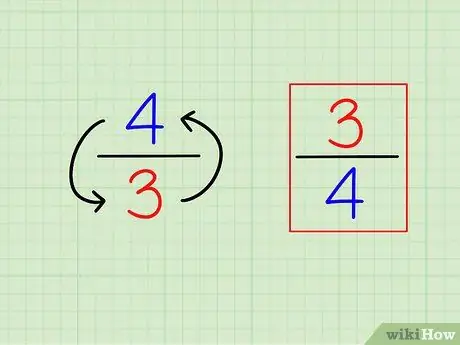
ขั้นตอนที่ 1. หาส่วนกลับของเศษส่วนโดยการกลับด้าน
คำจำกัดความของ "ส่วนกลับ" หรือตรงกันข้ามนั้นง่ายมาก ในการหาส่วนกลับของจำนวนเต็มใดๆ เพียงแค่คำนวณ "1 (ตัวเลขนั้น)" สำหรับเศษส่วน ส่วนกลับนั้นเป็นเศษส่วนที่แตกต่างกัน กล่าวคือ ตัวเลขจะ "กลับด้าน" (ผกผัน)
- ตัวอย่างเช่น ตรงข้ามกับ 3/4 เป็น 4/3.
- จำนวนใด ๆ เมื่อคูณด้วยผลตอบแทน 1
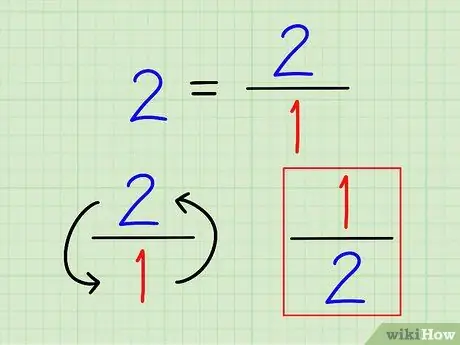
ขั้นตอนที่ 2 เขียนส่วนกลับของจำนวนเต็มเป็นเศษส่วน
ส่วนกลับของตัวเลขจะเป็น 1 เสมอ (ตัวเลขนั้น) สำหรับจำนวนเต็ม ให้เขียนเป็นเศษส่วน ไม่มีประโยชน์ในการคำนวณตัวเลขนั้นเป็นทศนิยม
ตัวอย่างเช่น ส่วนกลับของ 2 คือ 1 2 = 1/2.
วิธีที่ 2 จาก 3: การหาค่าผกผันของเศษส่วนผสม
ขั้นตอนที่ 1 ระบุจำนวนคละ
เศษส่วนผสมประกอบด้วยจำนวนเต็มและเศษส่วน เช่น 24/5. มีสองขั้นตอนในการหาส่วนกลับของจำนวนคละดังที่อธิบายไว้ด้านล่าง
ขั้นตอนที่ 2 แปลงจำนวนคละให้เป็นเศษเกิน
จำไว้ว่า 1 สามารถเขียนเป็น (ตัวเลข)/(ตัวเลขเดียวกัน) ได้เสมอ และเศษส่วนที่มีตัวส่วนเท่ากัน (เลขล่าง) รวมกันได้ นี่คือตัวอย่างการใช้24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
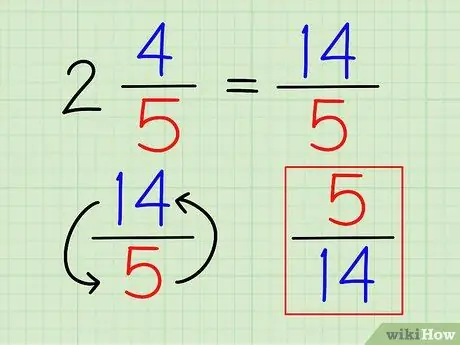
ขั้นตอนที่ 3 พลิกเศษส่วน
เมื่อตัวเลขถูกเขียนเป็นเศษส่วนแล้ว คุณสามารถหาส่วนกลับได้เช่นเดียวกับเศษส่วนอื่นๆ โดยการกลับเศษส่วน
ในตัวอย่างข้างต้น ส่วนกลับของ 14/5 เป็น 5/14.
วิธีที่ 3 จาก 3: การหาค่าตรงข้ามของทศนิยม
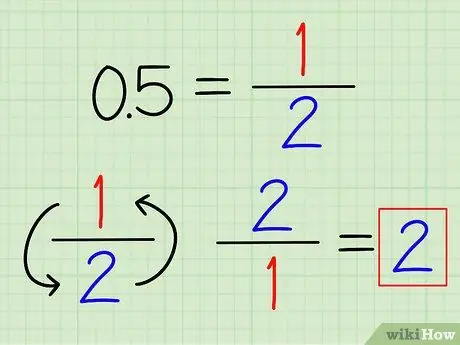
ขั้นตอนที่ 1 แปลงทศนิยมเป็นเศษส่วนถ้าเป็นไปได้
คุณอาจจำตัวเลขทศนิยมที่ใช้บ่อยได้ ซึ่งสามารถแปลงเป็นเศษส่วนได้อย่างง่ายดาย ตัวอย่างเช่น 0.5 = 1/2 และ 0.25 = 1/4. เมื่อทศนิยมถูกแปลงเป็นเศษส่วนแล้ว ให้พลิกเศษส่วนเพื่อหาส่วนกลับ
ตัวอย่างเช่น ส่วนกลับของ 0.5 คือ 2/1 = 2.
ขั้นตอนที่ 2 เขียนปัญหาการหาร
หากคุณไม่สามารถแปลงเป็นเศษส่วนได้ ให้คำนวณส่วนกลับของตัวเลขในรูปของปัญหาการหาร: 1 (ทศนิยม) คุณสามารถใช้เครื่องคิดเลขเพื่อแก้ปัญหาหรือดำเนินการในขั้นตอนต่อไปเพื่อแก้ปัญหาด้วยตนเอง
ตัวอย่างเช่น คุณสามารถหาส่วนกลับของ 0.4 ได้โดยการคำนวณ 1 0.4
ขั้นตอนที่ 3 เปลี่ยนโจทย์การหารเป็นจำนวนเต็ม
ขั้นตอนแรกในการหารทศนิยมคือการย้ายจุดทศนิยมจนกว่าตัวเลขทั้งหมดจะเป็นจำนวนเต็ม ตราบใดที่คุณย้ายจุดทศนิยมของตัวเลขทั้งสองด้วยจำนวนขั้นตอนเท่ากัน คุณจะได้คำตอบที่ถูกต้อง
ตัวอย่างเช่น คุณสามารถใช้ 1 0, 4 และเขียนใหม่เป็น 10 4 ในกรณีนี้ คุณย้ายตำแหน่งทศนิยมทั้งหมดไปทางขวาหนึ่งขั้น เช่นเดียวกับที่คุณคูณตัวเลขแต่ละตัวด้วยสิบ
ขั้นตอนที่ 4 แก้ปัญหาโดยใช้การหารยาว
ใช้วิธีหารยาวในการคำนวณส่วนกลับ ถ้านับ 10 4 จะได้คำตอบ 2, 5 ซึ่งเป็นส่วนกลับของ 0, 4
เคล็ดลับ
- ส่วนกลับติดลบของจำนวนนั้นเหมือนกับส่วนกลับปกติ คือ คูณด้วยค่าลบหนึ่ง ตัวอย่างเช่น ส่วนกลับเชิงลบของ 3/4 เป็น -4/3.
- ส่วนกลับหรือส่วนกลับมักเรียกว่า "ผกผันการคูณ"
- เลข 1 อยู่ตรงข้ามตัวมันเองเพราะ 1 1 = 1
- หมายเลข 0 ไม่มีส่วนกลับเพราะ 0 ไม่ได้กำหนดไว้