การหารเศษส่วนด้วยจำนวนเต็มไม่ยากอย่างที่คิด ในการหารเศษส่วนด้วยจำนวนเต็ม สิ่งที่คุณต้องทำคือแปลงจำนวนเต็มเป็นเศษส่วน หาส่วนกลับของเศษส่วน แล้วคูณผลลัพธ์ด้วยเศษส่วนแรก หากคุณต้องการทราบวิธีการทำ เพียงทำตามขั้นตอนเหล่านี้:
ขั้นตอน
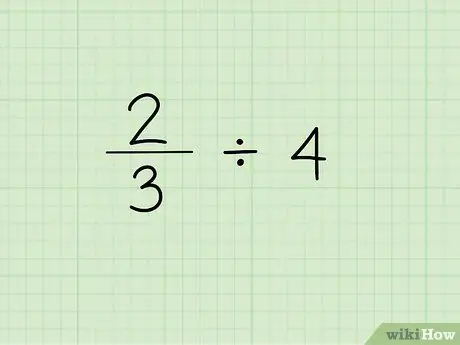
ขั้นตอนที่ 1. เขียนปัญหา
ขั้นตอนแรกในการหารเศษส่วนด้วยจำนวนเต็มคือการเขียนเศษส่วนตามด้วยเครื่องหมายหารและจำนวนเต็มที่คุณต้องหารเศษส่วน สมมติว่าเรากำลังแก้ไขปัญหาต่อไปนี้: 2/3 4.
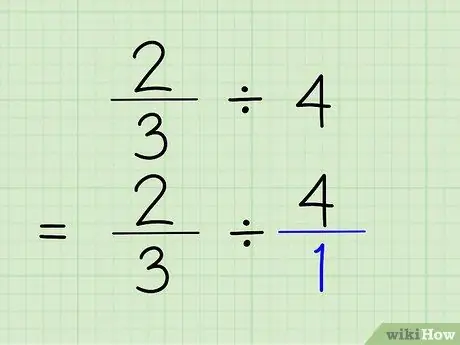
ขั้นตอนที่ 2 แปลงจำนวนเต็มเป็นเศษส่วน
ในการแปลงจำนวนเต็มเป็นเศษส่วน สิ่งที่คุณต้องทำคือวางจำนวนเต็มไว้เหนือเลข 1 เลขจำนวนเต็มจะกลายเป็นตัวเศษและ 1 จะกลายเป็นตัวส่วนของเศษส่วน การพูด 4/1 นั้นเหมือนกับการพูด 4 จริงๆ เพราะคุณจะแสดงเพียงว่าตัวเลขนั้นมี "1" 4 ครั้งเท่านั้น ปัญหาจะอยู่ที่ 2/3 4/1
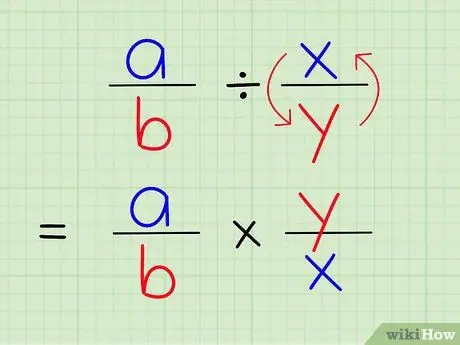
ขั้นตอนที่ 3 การหารเศษส่วนด้วยส่วนอื่นก็เหมือนกับการคูณเศษส่วนนั้นด้วยส่วนกลับของเศษส่วนอื่น
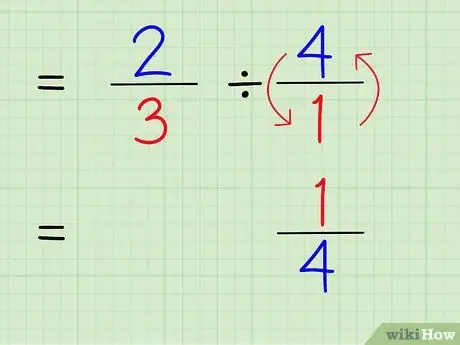
ขั้นตอนที่ 4 เขียนส่วนกลับของจำนวนเต็ม
ในการหาส่วนกลับของจำนวน ให้สลับตัวเศษและตัวส่วนของจำนวนนั้น ดังนั้น ในการหาส่วนกลับของ 4/1 เพียงแค่สลับตัวเศษและส่วนเพื่อให้จำนวนกลายเป็น 1/4
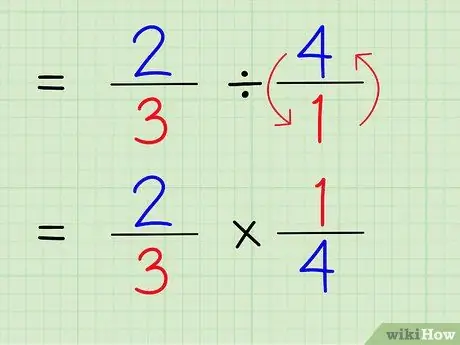
ขั้นตอนที่ 5. เปลี่ยนเครื่องหมายหารเป็นเครื่องหมายคูณ
ปัญหาจะอยู่ที่ 2/3 x 1/4
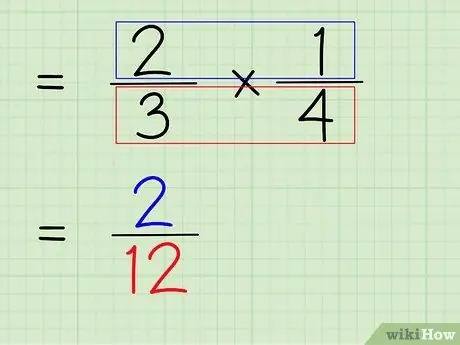
ขั้นตอนที่ 6 คูณตัวเศษและตัวส่วนของเศษส่วน
ดังนั้น ขั้นตอนต่อไปคือการคูณตัวเศษและตัวส่วนของเศษส่วนเพื่อให้ได้ตัวเศษและตัวส่วนใหม่เป็นคำตอบสุดท้าย
- ในการคูณตัวเศษ ก็แค่คูณ 2 x 1 ได้ 2
- ในการคูณตัวส่วน ก็แค่คูณ 3 x 4 ได้ 12
- 2/3 x 1/4 = 2/12
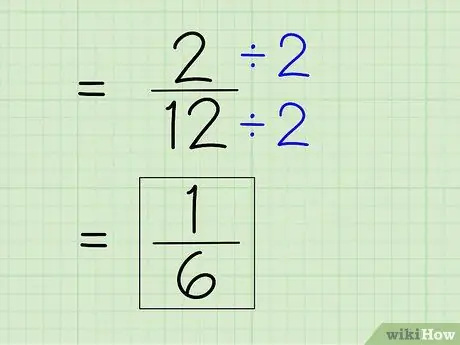
ขั้นตอนที่ 7 ลดความซับซ้อนของเศษส่วน
ในการทำให้เศษส่วนง่ายขึ้น คุณต้องหาตัวหารที่เล็กที่สุด ซึ่งหมายความว่าคุณต้องหารตัวเศษและตัวส่วนด้วยจำนวนใดๆ ที่หารจำนวนทั้งสองได้ เนื่องจาก 2 เป็นตัวเศษ คุณจะต้องดูว่า 2 สามารถหาร 12 ได้ทั้งหมดหรือไม่ -- เพราะ 12 เป็นเลขคู่ จากนั้นหารตัวเศษและตัวส่วนด้วย 2 เพื่อให้ได้ตัวเศษและตัวส่วนใหม่เพื่อให้ได้คำตอบง่ายๆ
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- เศษส่วน 2/12 สามารถลดรูปลงเหลือ 1/6 นี่คือคำตอบสุดท้ายของคุณ
เคล็ดลับ
- นี่คือการช่วยจำ วิธีง่ายๆ ในการจำวิธีการคำนวณทั้งหมดเหล่านี้ จำไว้ว่า: "มันง่ายที่จะหารเศษส่วน กลับเลขที่สองแล้วคูณ!"
- อีกรูปแบบหนึ่งของวิธีการข้างต้นคือ JGB/JBG อย่าเปลี่ยนหมายเลขแรก เปลี่ยนเป็นการคูณ ย้อนกลับหมายเลขสุดท้าย หรือ B ก่อน ตามด้วย G
- หากคุณยกเลิกการคำนวณก่อนที่จะคูณมัน คุณอาจไม่จำเป็นต้องหารูปแบบเศษส่วนที่ง่ายที่สุดเพราะผลลัพธ์อยู่ในรูปแบบเศษส่วนที่ง่ายที่สุดอย่างที่คุณเห็นแล้ว ในตัวอย่างของเรา ก่อนที่เราจะคูณ 2/3 × 1/4 เราจะเห็นว่าตัวเศษแรก (2) และตัวส่วนที่สอง (4) มีตัวคูณเท่ากันของ 2 ซึ่งเราสามารถยกเลิกก่อนที่เราจะทำการคำนวณต่อไป สิ่งนี้แปลงปัญหาเป็น 1/3 × 1/2 ซึ่งให้ผลลัพธ์ 1/6 ทันทีและช่วยเราประหยัดเวลาในการทำให้เศษส่วนง่ายขึ้นในระยะต่อมา
- ถ้าเศษส่วนของคุณเป็นลบ วิธีนี้ก็ยังใช้ได้ ตรวจสอบให้แน่ใจว่าคุณได้ติดตามสัญญาณต่างๆ ในขณะที่คุณทำตามขั้นตอนเหล่านี้
