การนับเศษส่วนเป็นหนึ่งในทักษะทางคณิตศาสตร์ที่มีประโยชน์ที่สุดในการพัฒนา ก่อนทำการคำนวณเศษส่วน ให้เรียนรู้วิธีระบุส่วนและประเภทของเศษส่วน หลังจากนั้นคุณสามารถเพิ่มหรือลบได้ สำหรับการคำนวณที่ซับซ้อนมากขึ้น ให้เรียนรู้วิธีคูณและหารเศษส่วน โดยปกติ คุณจะต้องลดรูปหรือลดเศษส่วนด้วย
ขั้นตอน
วิธีที่ 1 จาก 4: การจำแนกเศษส่วน
ขั้นตอนที่ 1 หาเศษส่วน
เศษส่วนเขียนเป็นตัวเลขหนึ่งตัวเหนือเส้นแบ่ง และอีกตัวหนึ่งอยู่ใต้เส้น
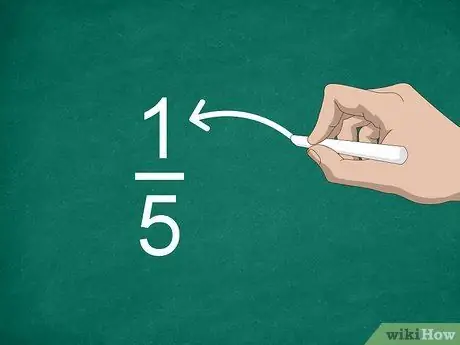
ขั้นตอนที่ 2 ระบุตัวเศษ
ตัวเลขเหนือเส้นเรียกว่า ตัวเศษ และแสดงว่าเศษส่วนมีกี่ส่วน
ตัวอย่างเช่น ในเศษส่วน 1/5 “1” เป็นตัวเศษ
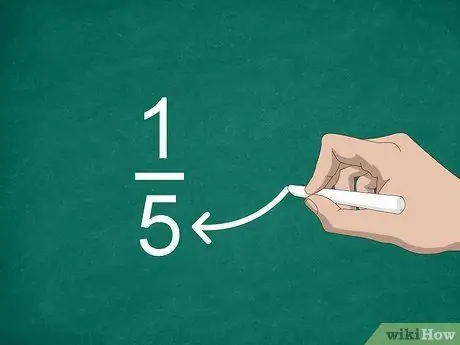
ขั้นตอนที่ 3 ค้นหาตัวส่วน
ตัวเลขที่อยู่ด้านล่างเส้นเรียกว่าตัวส่วน ค่านี้ระบุจำนวนส่วนที่ "สร้าง" เป็นจำนวนเต็ม
ตัวอย่างเช่น ในเศษส่วน 1/5 "5" เป็นตัวส่วน ดังนั้นจึงมีเศษส่วนห้าส่วน
ขั้นตอนที่ 4 กำหนดว่าเศษส่วนเป็นเศษส่วนที่เหมาะสมหรือเศษส่วนไม่เหมาะสม
ถ้าตัวเศษน้อยกว่าตัวส่วน เศษส่วนนั้นเป็นเศษส่วนธรรมชาติ เศษส่วนที่ไม่เหมาะสม ตัวเศษมากกว่าตัวส่วน
- ตัวอย่างเช่น 3/4 เป็นเศษส่วนที่สมเหตุสมผลและ 5/3 เป็นเศษส่วนที่ไม่เหมาะสม
- หากคุณมีจำนวนเต็มที่มีเศษส่วน ตัวเลขนั้นเรียกว่าจำนวนคละ ตัวอย่างเช่น 1 1/2 เป็นจำนวนคละ
วิธีที่ 2 จาก 4: เพิ่มหรือลบเศษส่วน
ขั้นตอนที่ 1 ระบุเศษส่วนที่มีตัวส่วนเท่ากัน
หากคุณต้องการบวกหรือลบเศษส่วน เศษส่วนแต่ละส่วนจะต้องมีตัวส่วนเหมือนกันก่อนที่คุณจะคำนวณ สังเกตตัวส่วนของเศษส่วนแต่ละส่วนเพื่อให้แน่ใจว่าทั้งหมดเท่ากัน (คล้ายกัน)
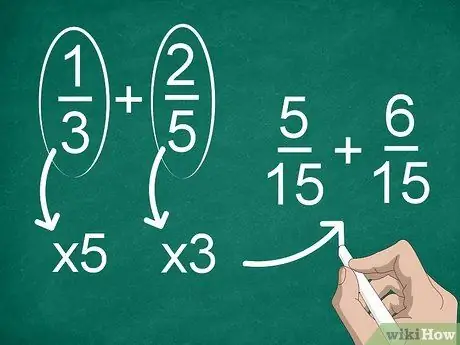
ขั้นตอนที่ 2 หาตัวส่วนร่วมหากเศษส่วนแต่ละตัวมีตัวส่วนต่างกัน
ถ้าตัวส่วนไม่เหมือนกัน คุณจะต้องเปลี่ยนเศษส่วนให้มีตัวส่วนเหมือนกัน ในการหาตัวส่วนร่วม ให้คูณเศษส่วนแต่ละตัวด้วยตัวส่วนของอีกตัวหนึ่ง
ตัวอย่างเช่น ในการหาตัวส่วนร่วมใน 1/3 + 2/5 ให้คูณ "1" กับ "3" ด้วย "5" แล้วคูณ "2" กับ "5" ด้วย "3" ตอนนี้ คุณมีการบวก 5/15 + 6/15 หลังจากนั้นคุณสามารถคำนวณเศษส่วนได้
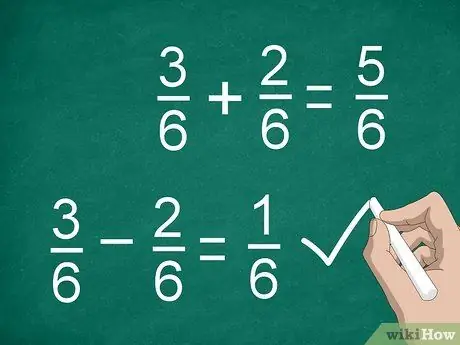
ขั้นตอนที่ 3 บวกหรือลบตัวเศษเพื่อคำนวณเศษส่วน
เมื่อคุณพบตัวส่วนร่วมและคูณตัวเศษแล้ว (ถ้าจำเป็น) คุณก็พร้อมที่จะบวกหรือลบ บวกหรือลบตัวเศษและวางผลลัพธ์ไว้เหนือเส้นแบ่ง เขียนตัวส่วนร่วมใต้บรรทัด
- ตัวอย่างเช่น 3/6 - 2/6 = 1/6
- อย่าบวกหรือลบตัวส่วน
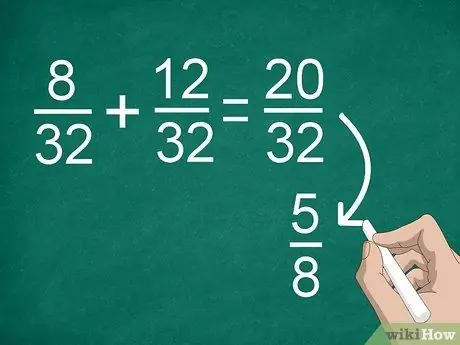
ขั้นตอนที่ 4 ลดความซับซ้อนของผลลัพธ์หากจำเป็น
ถ้าก่อนหน้านี้คุณจำเป็นต้องหาตัวส่วนร่วม คุณอาจได้เศษส่วนขนาดใหญ่ที่ลดรูปได้ ตัวอย่างเช่น หากคุณเพิ่ม 8/32 +12/32 คุณจะได้ “20/32” เป็นผลลัพธ์ เศษส่วนนี้สามารถย่อเป็น “5/8”
วิธีที่ 3 จาก 4: การคูณและลดความซับซ้อนของเศษส่วน
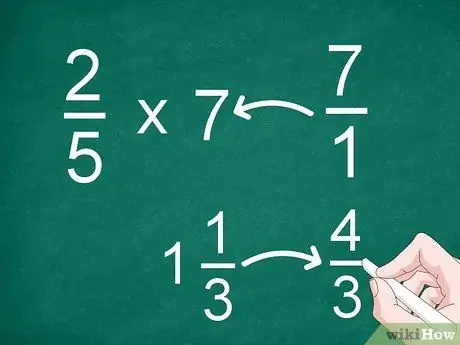
ขั้นตอนที่ 1 แปลงเศษส่วนผสมหรือจำนวนเต็มเป็นเศษส่วนที่ไม่เหมาะสม
เพื่อให้การคูณง่ายขึ้น คุณต้องแปลงตัวเลขแต่ละตัวให้เป็นเศษส่วนที่เหมาะสมหรือไม่เหมาะสม หากคุณมีจำนวนเต็มหรือจำนวนคละที่ต้องคูณ ขั้นแรกให้แปลงเป็นเศษส่วนร่วม (ธรรมชาติหรือไม่เหมาะสม)
- ตัวอย่างเช่น หากต้องการคูณ 2/5 ด้วย 7 ให้แปลง "7" เป็นเศษส่วน หลังจากนั้น คุณสามารถคูณ 2/5 ด้วย 7/1
- หากคุณมีจำนวนคละ เช่น 1 1/3 ให้แปลงเป็นเศษเกิน (“4/3”) ก่อนคูณ
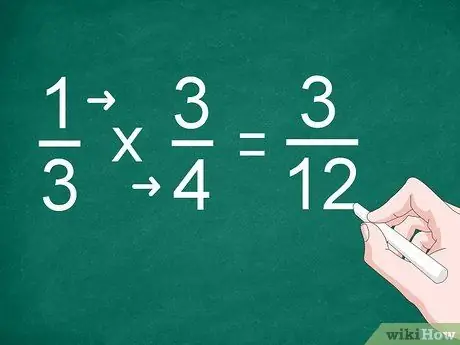
ขั้นตอนที่ 2 คูณแต่ละตัวเศษและส่วน
แทนที่จะบวก ให้คูณตัวเศษแล้วเขียนผลลัพธ์เหนือเส้นแบ่ง คุณต้องคูณตัวส่วนและเขียนผลลัพธ์ใต้บรรทัดด้วย
ตัวอย่างเช่น หากต้องการคูณ 1/3 ด้วย 3/4 ให้คูณ "1" ด้วย "3" เพื่อให้ได้ตัวเศษ คูณ “3” กับ “4” เพื่อให้ได้ตัวส่วน คำตอบของการคูณคือ "3/12"
ขั้นตอนที่ 3 ลดความซับซ้อนของผลลัพธ์
โดยปกติ คุณจะต้องลดผลลัพธ์ให้อยู่ในรูปแบบที่ง่ายกว่า โดยเฉพาะอย่างยิ่งถ้าคุณมีเศษส่วนผิดธรรมชาติในตอนแรก หาตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดและใช้ตัวประกอบนั้นเพื่อทำให้ตัวเศษและตัวส่วนง่ายขึ้น
ตัวอย่างเช่น สำหรับเศษส่วน 3/12 ตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดระหว่าง “3” และ “12” คือ “3” หารแต่ละองค์ประกอบของเศษส่วนด้วย "3" จนกว่าคุณจะได้เศษส่วน "1/4"
วิธีที่ 4 จาก 4: หารเศษส่วน
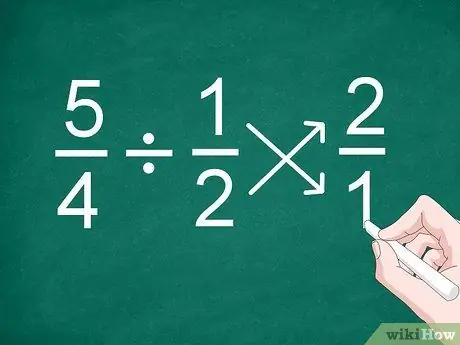
ขั้นตอนที่ 1 กลับตำแหน่งของเศษส่วนที่สอง
วิธีที่ง่ายที่สุดในการหารเศษส่วน แม้แต่เศษส่วนที่มีตัวส่วนต่างกัน คือการกลับตำแหน่งของเศษส่วนที่สองก่อนที่คุณจะคำนวณผลลัพธ์
ตัวอย่างเช่น สำหรับปัญหา 5/4 1/2 ให้กลับตำแหน่งของเศษส่วน "1/2" ให้เป็น "2/1"
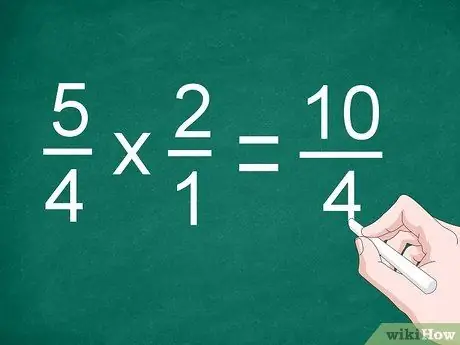
ขั้นตอนที่ 2 คูณทั้งเศษและส่วน
คูณเศษส่วนโดยตรงเพื่อคูณตัวเศษ เขียนผลลัพธ์เหนือเส้นแบ่ง แล้วคูณตัวส่วน บันทึกผลคูณของตัวส่วนใต้บรรทัด
จากตัวอย่างก่อนหน้านี้ คูณ 5/4 ด้วย 2/1 เพื่อให้ได้ “10/4”
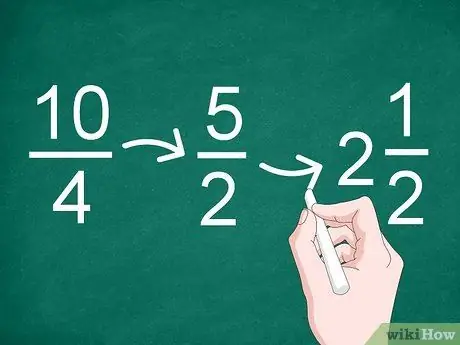
ขั้นตอนที่ 3 ลดความซับซ้อนของผลลัพธ์หากจำเป็น
หากผลการหารเป็นเศษเกินหรือลดได้ ให้ทอนเศษส่วนให้ง่ายขึ้น ใช้ตัวประกอบร่วมมากเพื่อลดเศษส่วน
- ตัวอย่างเช่น ตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดในเศษส่วน 10/4 คือ “2” ดังนั้นผลลัพธ์ของการลดความซับซ้อนจึงกลายเป็น “5/2” (10 หารด้วย 2 และ 4 หารด้วย 2)
- เนื่องจากผลลัพธ์ของการลดสัดส่วนเป็นเศษส่วนที่ไม่เหมาะสม คุณจึงสามารถแปลงเป็นจำนวนเต็มและเศษส่วน (จำนวนคละ) ได้ ดังนั้น 5/2 สามารถเปลี่ยนเป็น “2” ได้
เคล็ดลับ
- หากคุณกำลังใช้เศษส่วนเชิงซ้อน คุณจะต้องทำตามขั้นตอนเพิ่มเติมเพื่อทำให้เศษส่วนง่ายขึ้น อย่างไรก็ตาม การทำให้เข้าใจง่ายนี้เองเป็นส่วนบังคับของกระบวนการคำนวณ
- เขียนเศษส่วนให้เรียบร้อยเสมอเพื่อลดความเสี่ยงในการคำนวณผิด
