สำหรับคนส่วนใหญ่ เศษส่วนเป็นการคำนวณที่ซับซ้อนเป็นลำดับแรก แนวคิดเรื่องเศษส่วนนั้นค่อนข้างยากและคุณต้องเรียนรู้เงื่อนไขพิเศษก่อน เนื่องจากเศษส่วนมีกฎพิเศษสำหรับการบวก การลบ การคูณ และการหาร หลายคนจึงสับสน อย่างไรก็ตาม ด้วยการฝึกฝนมากมาย ทุกคนสามารถเรียนรู้และทำการคำนวณที่เกี่ยวข้องกับเศษส่วนได้
ขั้นตอน
วิธีที่ 1 จาก 5: การทำความเข้าใจเศษส่วน
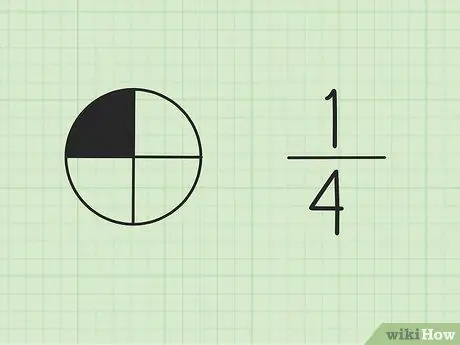
ขั้นตอนที่ 1 เข้าใจว่าเศษส่วนเป็นส่วนหนึ่งของทั้งหมด
ตัวเลขที่อยู่ด้านบนเรียกว่าตัวเศษ และแสดงถึงจำนวนส่วนของผลรวม ตัวเลขที่อยู่ด้านล่างเรียกว่าตัวส่วน ซึ่งแสดงถึงจำนวนชิ้นส่วนทั้งหมด
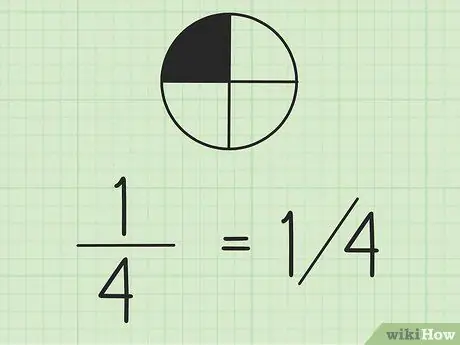
ขั้นตอนที่ 2 จำไว้ว่าคุณสามารถเขียนเศษส่วนโดยใช้เครื่องหมายทับ
ตัวเลขทางซ้ายเป็นตัวเศษ และตัวเลขทางขวาเป็นตัวส่วน หากคุณกำลังใช้เศษส่วนในบรรทัดเดียวกัน จะเป็นความคิดที่ดีที่จะเขียนตัวเศษไว้เหนือตัวส่วน
ตัวอย่างเช่น ถ้าคุณเอาพิซซ่าชิ้นหนึ่งในสี่ชิ้น แสดงว่าคุณมีพิซซ่า หากคุณมีพิซซ่า 7/3 ถาด แสดงว่าคุณมีพิซซ่าทั้งหมด 2 ถาด บวก 1 ใน 3 พิซซ่าแผ่น
วิธีที่ 2 จาก 5: ความแตกต่างระหว่างเศษส่วนผสมและเศษส่วนง่าย
ขั้นตอนที่ 1 ทำความเข้าใจว่าจำนวนคละประกอบด้วยจำนวนเต็มและเศษส่วน เช่น 2 1/3 หรือ 45 1/2
โดยปกติ คุณต้องแปลงจำนวนคละให้อยู่ในรูปแบบที่ง่ายกว่าในการบวก ลบ คูณ หรือหาร
ขั้นตอนที่ 2 เปลี่ยนจำนวนคละโดยการคูณจำนวนเต็มด้วยตัวส่วนในเศษส่วน แล้วบวกด้วยตัวเศษ
เขียนผลลัพธ์เป็นตัวเศษ ในขณะที่ตัวส่วนไม่เปลี่ยนแปลง
ตัวอย่างเช่น ในการแปลง 2 1/3 เป็นเศษส่วนอย่างง่าย ให้คูณ 2 ด้วย 3 แล้วบวก 1 และรับ 7/3
ขั้นตอนที่ 3 แปลงเศษส่วนอย่างง่ายเป็นจำนวนคละโดยหารตัวเศษด้วยตัวส่วน
ผลลัพธ์ทั้งหมดของการหารจะถูกเขียนเป็นจำนวนเต็ม และส่วนที่เหลือของการหารจะถูกเขียนเป็นตัวเศษของเศษส่วน ตัวส่วนไม่เปลี่ยนแปลง
ตัวอย่างเช่น ในการแปลง 7/3 เป็นจำนวนคละ ให้หาร 7 ด้วย 3 เพื่อให้ได้ 2 ด้วยเศษเหลือ 1 ดังนั้นจำนวนคละคือ 2 1/3 เศษส่วนอย่างง่ายสามารถแปลงเป็นจำนวนคละได้ก็ต่อเมื่อตัวเศษมากกว่าตัวส่วน
วิธีที่ 3 จาก 5: การบวกและการลบเศษส่วน
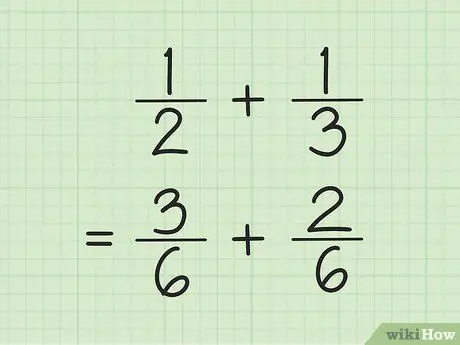
ขั้นตอนที่ 1 หาตัวส่วนร่วมเพื่อบวกและลบเศษส่วน
เคล็ดลับ คูณตัวเลขในตัวส่วน แล้วคูณตัวเศษแต่ละตัวด้วยตัวเลขที่ใช้หาตัวส่วน บางครั้ง คุณสามารถหา LCM (ตัวคูณร่วมน้อย) สำหรับตัวส่วนได้โดยการคูณตัวส่วนเข้าด้วยกัน
ตัวอย่างเช่น ในการเพิ่มและ 1/3 ก่อนอื่นให้หา LCM (ตัวคูณร่วมน้อย) ของตัวส่วนสองตัวโดยการคูณกัน ดังนั้น คุณคูณ 2 กับ 3 เพื่อให้ได้ LCM 6 คูณ 1 ด้วย 3 เพื่อให้ได้ 3 เป็นตัวเศษใหม่ของเศษส่วนแรก คูณ 1 ด้วย 2 เพื่อให้ได้ 2 เป็นตัวเศษใหม่ของเศษส่วนที่สอง เศษส่วนใหม่ของคุณคือ 3/6 และ 2/6
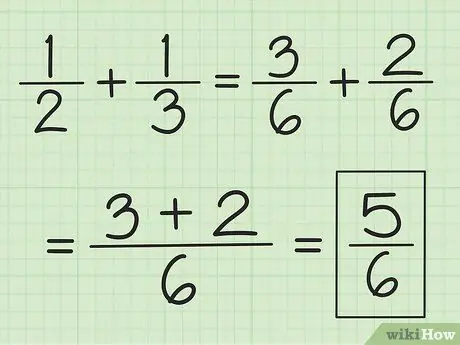
ขั้นตอนที่ 2 เพิ่มตัวเศษสองตัวเข้าด้วยกันและอย่าเปลี่ยนตัวส่วน
ตัวอย่างเช่น 3/6 บวก 2/6 คือ 5/6 และ 2/6 บวก 1/6 คือ 3/6
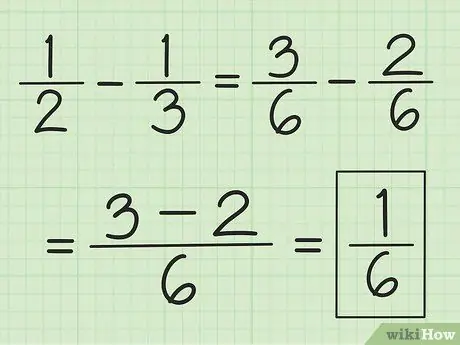
ขั้นตอนที่ 3 ใช้เทคนิคที่คล้ายกันสำหรับการลบ
หา LCM ของตัวส่วนก่อน แต่แทนที่จะบวกกัน ให้ลบตัวเลขของตัวเศษแรกด้วยจำนวนที่สอง
ตัวอย่างเช่น หากต้องการลบ 1/3 จาก 1/2 ก่อนอื่นให้เปลี่ยนเศษส่วนเป็น 3/6 และ 2/6 จากนั้นลบ 3 ด้วย 2 เพื่อให้ได้ 1 ซึ่งส่งผลให้ 1/6
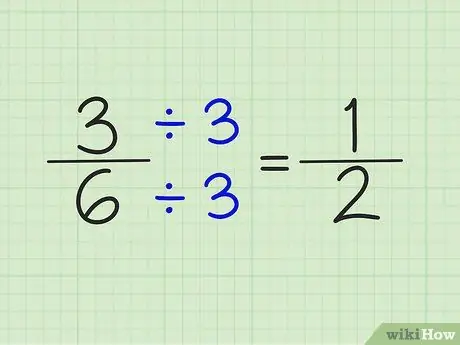
ขั้นตอนที่ 4 ลดความซับซ้อนของเศษส่วนโดยหารตัวเศษและตัวส่วนด้วยจำนวนเดียวกัน
ตัวอย่างเช่น ตัวเลข 5/6 ไม่สามารถลดความซับซ้อนได้ อย่างไรก็ตาม 3/6 สามารถทำให้ง่ายขึ้นได้โดยการหารตัวเศษและส่วนด้วยเลข 3 ผลลัพธ์คือเศษส่วนของ 1/2
ขั้นตอนที่ 5. แปลงเศษส่วนเป็นจำนวนคละถ้าตัวเศษมากกว่าตัวส่วน
วิธีที่ 4 จาก 5: การคูณและหารเศษส่วน
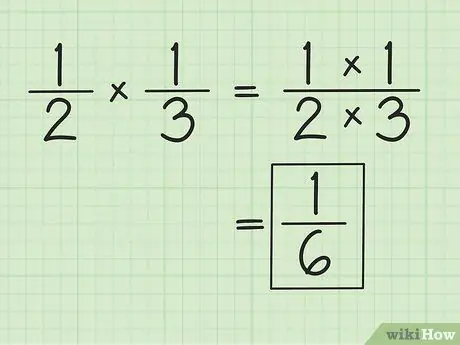
ขั้นตอนที่ 1 คูณตัวเศษและส่วนแยกกันเพื่อคูณเศษส่วน
ตัวอย่างเช่น เมื่อคูณกับ 1/3 ผลลัพธ์จะเป็น 1/6 (1 คูณ 1 และ 2 คูณ 3) คุณไม่จำเป็นต้องจับคู่ตัวส่วนเมื่อคูณเศษส่วน ลดความซับซ้อนหรือแก้ไขผลลัพธ์ที่ได้รับ หากจำเป็น
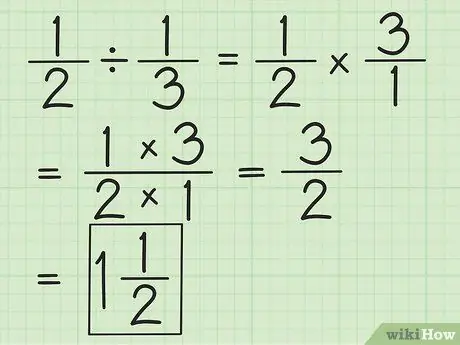
ขั้นตอนที่ 2 หารเศษส่วนสองส่วนโดยกลับเศษส่วนที่สอง จากนั้นคูณทั้งสอง
ตัวอย่างเช่น หากคุณต้องการหาร 1/2 ด้วย 1/3 ให้กลับเศษส่วนที่สองเป็น 3/1 ก่อน คูณด้วย 3/1 แล้วได้ 3/2 ลดความซับซ้อนของเศษส่วนหรือแปลงเป็นจำนวนคละ ถ้าเป็นไปได้
วิธีที่ 5 จาก 5: การทำงานกับเศษส่วนที่ซับซ้อน
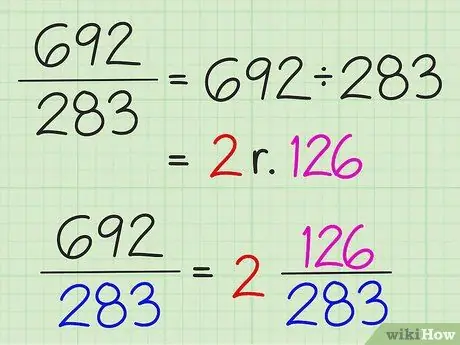
ขั้นตอนที่ 1 ใช้เศษส่วนทั้งหมดในลักษณะเดียวกัน แม้ว่าปัญหาจะดูซับซ้อนมาก
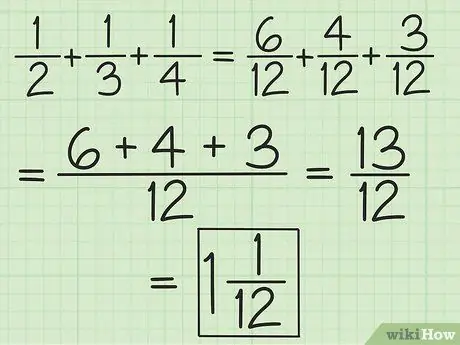
ขั้นตอนที่ 2 จับคู่ตัวส่วนสำหรับเศษส่วนทั้งหมดหรือทำงานเป็นคู่โดยเริ่มจากซ้ายไปขวาเพื่อเพิ่มและลบเศษส่วนมากกว่าสองส่วน
ตัวอย่างเช่น หากต้องการบวก 1/2, 1/3 และ 1/4 คุณสามารถเปลี่ยนเป็น 6/12, 4/12 และ 3/12 เพื่อให้ได้ 13/12 หรือเพิ่ม 3/6 และ 2 ได้ /6 คุณจะได้ 5/6 แล้วบวก 5/6 กับ 1/4 (ทำให้ตัวส่วนเท่ากัน เศษส่วนที่สองกลายเป็น 3/12) เพื่อให้ได้ 13/12 (10/12 บวก 3/12) แปลงเป็นจำนวนคละ ซึ่งก็คือ 1 1/12
เคล็ดลับ
- จำไว้ว่าคุณได้เรียนรู้คณิตศาสตร์ค่อนข้างมาก คณิตศาสตร์เป็นเหมือนภาษาที่คุณออกเสียงได้คล่อง และตอนนี้คุณกำลังพยายามเรียนรู้ที่จะอ่านและเขียน
- อย่าลืมทำให้ผลลัพธ์สุดท้ายของการคำนวณง่ายขึ้นเสมอ ไม่ว่าปัญหาของคุณจะอยู่ในรูปของเศษส่วนธรรมดา ตัวเลขคละ หรือเศษส่วนเชิงซ้อน
