IQR คือช่วงระหว่างควอไทล์หรือช่วงรากของควอร์ไทล์ของชุดข้อมูล IQR ใช้ในการวิเคราะห์ทางสถิติเพื่อช่วยสรุปเกี่ยวกับชุดข้อมูล IQR ถูกใช้บ่อยกว่าช่วงเนื่องจาก IQR ไม่รวมข้อมูลนอกสุด อ่านต่อเพื่อเรียนรู้วิธีค้นหา IQR!
ขั้นตอน
วิธีที่ 1 จาก 3: การทำความเข้าใจ IQR
ขั้นตอนที่ 1. เข้าใจวิธีใช้ IQR
โดยพื้นฐานแล้ว IQR เป็นวิธีการทำความเข้าใจการแพร่กระจายของชุดตัวเลข ช่วงควอร์ไทล์รากถูกกำหนดเป็นความแตกต่างระหว่างควอไทล์บน (25% บนสุด) และควอไทล์ล่าง (ต่ำสุด 25%) ของชุดข้อมูล
เคล็ดลับ:
ควอไทล์ล่างมักจะเขียนเป็น Q1 และควอไทล์บนเขียนเป็น Q3 ซึ่งในทางเทคนิคจะทำให้จุดกึ่งกลางของข้อมูลเป็น Q2 และจุดสูงสุดจะเป็น Q4
ขั้นตอนที่ 2 ทำความเข้าใจควอร์ไทล์
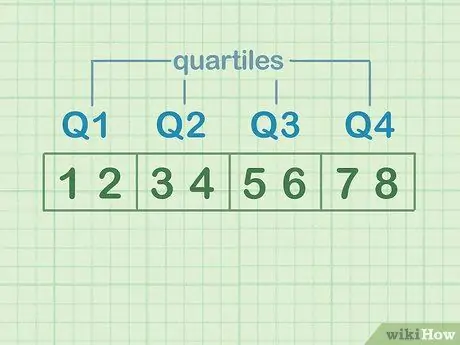
เพื่อแสดงควอร์ไทล์ ให้แบ่งชุดของตัวเลขออกเป็นสี่ส่วนเท่าๆ กัน แต่ละส่วนเหล่านี้เป็น "ควอร์ไทล์" สมมติว่าชุดข้อมูลคือ: 1, 2, 3, 4, 5, 6, 7, 8
- 1 และ 2 เป็นควอร์ไทล์แรกหรือ Q1
- 3 และ 4 เป็นควอร์ไทล์ที่สองหรือ Q2
- 5 และ 6 เป็นควอร์ไทล์ที่สามหรือ Q3
- 7 และ 8 เป็นควอร์ไทล์ที่สี่หรือ Q4
ขั้นตอนที่ 3 เรียนรู้สูตร
ในการค้นหาความแตกต่างระหว่างควอร์ไทล์บนและควอไทล์ล่าง คุณต้องลบเปอร์เซ็นไทล์ที่ 75 ออกจากเปอร์เซ็นไทล์ที่ 25
สูตรนี้เขียนว่า: Q3 – Q1 = IQR
วิธีที่ 2 จาก 3: การคอมไพล์ชุดข้อมูล
ขั้นตอนที่ 1 รวบรวมข้อมูลของคุณ
หากคุณศึกษา IQR ในชั้นเรียนและในการทดสอบ คุณอาจได้รับชุดข้อมูลที่เตรียมไว้แล้ว เช่น 1, 4, 5, 7, 10 นี่คือชุดข้อมูลของคุณ – ตัวเลขที่คุณจะใช้ อย่างไรก็ตาม คุณสามารถสร้างตัวเลขของคุณเองจากคำถามเกี่ยวกับตารางหรือปัญหาเรื่องเรื่องราวได้
ตรวจสอบให้แน่ใจว่าแต่ละตัวเลขแสดงถึงสิ่งเดียวกัน:
ตัวอย่างเช่น จำนวนไข่ในแต่ละรังของประชากรนกที่กำหนด หรือจำนวนที่จอดรถในแต่ละบ้านในบล็อกที่ระบุ
ขั้นตอนที่ 2 จัดเรียงข้อมูลของคุณตามลำดับจากน้อยไปมาก
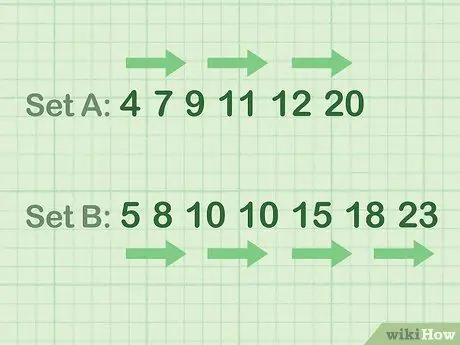
กล่าวอีกนัยหนึ่ง: จัดเรียงตัวเลขจากน้อยไปมาก ใช้คำแนะนำจากตัวอย่างต่อไปนี้
- ตัวอย่างข้อมูลเลขคู่ (Set A): 4 7 9 11 12 20
- ตัวอย่างข้อมูลเลขคี่ (Set B): 5 8 10 10 15 18 23
ขั้นตอนที่ 3 แบ่งข้อมูลออกเป็นสองส่วน
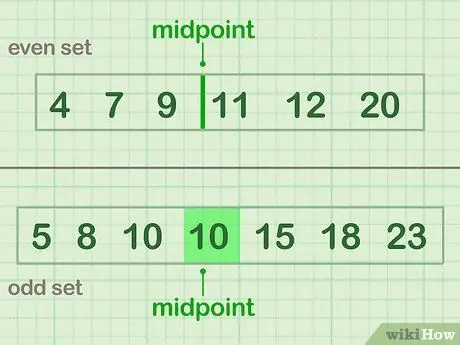
หากต้องการแบ่งครึ่ง ให้ค้นหาจุดกึ่งกลางของข้อมูล: ตัวเลขหรือตัวเลขที่อยู่ตรงกลางชุดข้อมูล หากคุณมีข้อมูลเป็นจำนวนคี่ ให้เลือกตัวเลขที่อยู่ตรงกลาง หากคุณมีข้อมูลเป็นจำนวนคู่ จุดกึ่งกลางจะอยู่ระหว่างตัวเลขที่อยู่ตรงกลางมากที่สุดสองตัว
- ตัวอย่างคู่ (Set A) ซึ่งมีจุดกึ่งกลางระหว่าง 9 ถึง 11: 4 7 9 | 11 12 20
- ตัวอย่างคี่ (Set B) ซึ่งมีจุดกึ่งกลางของค่า (10): 5 8 10 (10) 15 18 23
วิธีที่ 3 จาก 3: การคำนวณ IQR
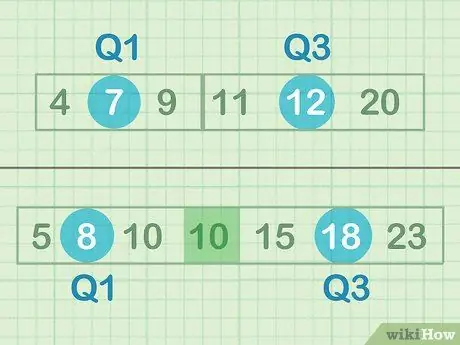
ขั้นตอนที่ 1 ค้นหาค่ามัธยฐานของข้อมูลครึ่งล่างและบนของคุณ
ค่ามัธยฐานคือ "จุดกึ่งกลาง" หรือตัวเลขที่อยู่ตรงกลางของชุดตัวเลข ในกรณีนี้ คุณไม่ได้มองหาจุดกึ่งกลางของตัวเลขทั้งหมด แต่กำลังมองหาจุดกึ่งกลางสัมพัทธ์ของชุดย่อยข้อมูลบนและล่าง หากคุณมีข้อมูลเป็นจำนวนคี่ อย่าใส่ตัวเลขตรงกลาง ตัวอย่างเช่น ในชุด B คุณไม่จำเป็นต้องรวม 10 ตัวเดียว
-
ตัวอย่างคู่ (ชุด A):
- ค่ามัธยฐานของครึ่งล่างของข้อมูล = 7 (Q1)
- ค่ามัธยฐานของครึ่งบนของข้อมูล = 12 (Q3)
-
ตัวอย่างคี่ (ชุด B):
- ค่ามัธยฐานของข้อมูลครึ่งล่าง = 8 (Q1)
- ค่ามัธยฐานของครึ่งบนของข้อมูล = 18 (Q3)
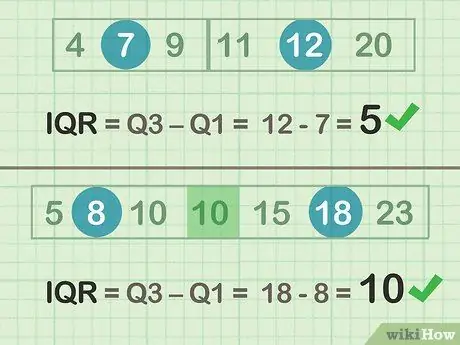
ขั้นตอนที่ 2 ลบ Q3-Q1 เพื่อกำหนด IQR
ตอนนี้คุณทราบจำนวนตัวเลขที่อยู่ระหว่างเปอร์เซ็นต์ไทล์ที่ 25 และ 75 คุณสามารถใช้หมายเลขนี้เพื่อทำความเข้าใจการแพร่กระจายของข้อมูล ตัวอย่างเช่น หากการทดสอบมีคะแนนสูงสุด 100 และ IQR ของคะแนนคือ 5 คุณสามารถสรุปได้ว่าคนส่วนใหญ่ที่ทำแบบทดสอบมีความเข้าใจตรงกันเกือบเท่ากัน เนื่องจากช่วงของเสียงสูงและต่ำนั้นไม่ใหญ่มาก อย่างไรก็ตาม หาก IQR ของคะแนนสอบเท่ากับ 30 คุณอาจเริ่มสงสัยว่าทำไมคนบางคนได้คะแนนสูงมาก และคนอื่นๆ ได้คะแนนต่ำมาก
- ตัวอย่างคู่ (ชุด A): 12 -7 = 5
- ตัวอย่างคี่ (ชุด B): 18 – 8 = 10
เคล็ดลับ
สิ่งสำคัญคือต้องเรียนรู้ที่จะทำสิ่งนี้ด้วยตัวเอง อย่างไรก็ตาม มีเครื่องคำนวณ IQR ออนไลน์หลายเครื่องที่คุณสามารถใช้ตรวจสอบงานของคุณได้ อย่าพึ่งพาแอพเครื่องคิดเลขมากเกินไปหากคุณเรียนรู้สิ่งนี้ในชั้นเรียน! หากระบบขอให้คุณค้นหา IQR ในการทดสอบ คุณจะต้องทราบวิธีค้นหาด้วยตนเอง
WikiHow ที่เกี่ยวข้อง
- วิธีการตรวจหาค่าผิดปกติ
- วิธีการคำนวณช่วงของชุดข้อมูล
- วิธีทำกล่องและไดอะแกรมเต็นท์