3 วิธีในการคำนวณความดันไอ

2024 ผู้เขียน: Jason Gerald | [email protected]. แก้ไขล่าสุด: 2024-02-01 14:16

คุณเคยทิ้งขวดน้ำไว้กลางแดดร้อนสักสองสามชั่วโมงแล้วได้ยินเสียง "ฟู่" เล็กน้อยเมื่อคุณเปิดมันหรือไม่? นี่เป็นเพราะหลักการที่เรียกว่าความดันไอ ในวิชาเคมี ความดันไอคือความดันที่กระทำโดยผนังของภาชนะปิดเมื่อสารเคมีในนั้นระเหย (กลายเป็นก๊าซ) ในการหาความดันไอที่อุณหภูมิที่กำหนด ให้ใช้สมการคลอสเซียส-แคลเปรอง: ln(P1/P2) = (ΔH_{ไอน้ำ}/R)((1/T2) - (1/T1)).

ขั้นตอน

วิธีที่ 1 จาก 3: การใช้สมการ Clausius-Clapeyron

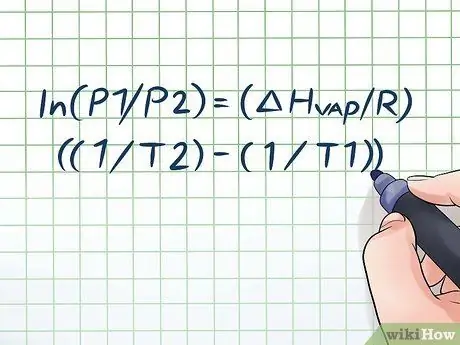
ขั้นตอนที่ 1 เขียนสมการคลอเซียส-คลาเปรองลงไป

สูตรที่ใช้ในการคำนวณความดันไอโดยการเปลี่ยนแปลงของความดันไอเมื่อเวลาผ่านไปเรียกว่าสมการคลอสเซียส–คลาเปยรอน (ตั้งชื่อตามนักฟิสิกส์รูดอล์ฟ คลอสเซียส และเบอนัวต์ ปอล ไมล แคลเปย์รอน) โดยพื้นฐานแล้วเป็นสูตรที่คุณจะต้องใช้ในการแก้ปัญหาส่วนใหญ่. คำถามเกี่ยวกับความดันไอมักพบในวิชาฟิสิกส์และเคมี สูตรเป็นแบบนี้: ln(P1/P2) = (ΔH_{ไอน้ำ}/R)((1/T2) - (1/T1)). ในสูตรนี้ ตัวแปรแสดงถึง:

• ชม_{ไอน้ำ}:

  เอนทาลปีของการกลายเป็นไอของของเหลว เอนทัลปีนี้มักจะพบได้ในตารางด้านหลังหนังสือเรียนวิชาเคมี

• NS:

  ค่าคงที่ก๊าซจริง/สากล หรือ 8.314 J/(K × Mol)

• ไตรมาสที่ 1:

  อุณหภูมิที่ทราบความดันไอ (หรืออุณหภูมิเริ่มต้น)

• T2:

  อุณหภูมิที่ไม่ทราบ/ต้องการหาความดันไอ (หรืออุณหภูมิสุดท้าย)

• P1 และ P2:

  ความดันไอที่อุณหภูมิ T1 และ T2 ตามลำดับ

ขั้นตอนที่ 2 ป้อนตัวแปรที่คุณรู้จัก

สมการคลอสเซียส-คลาเปรองดูซับซ้อนเพราะมีตัวแปรต่างกันมากมาย แต่จริงๆ แล้วไม่ยากถ้าคุณมีข้อมูลที่ถูกต้อง ปัญหาความดันไอขั้นพื้นฐานส่วนใหญ่จะระบุค่าอุณหภูมิสองค่าและค่าความดันหนึ่งค่าหรือค่าความดันสองค่าและค่าอุณหภูมิหนึ่งค่า - เมื่อคุณเข้าใจแล้วการแก้สมการนี้ทำได้ง่ายมาก

• ตัวอย่างเช่น สมมติว่าเรามีภาชนะที่เต็มไปด้วยของเหลวที่อุณหภูมิ 295 K ซึ่งความดันไอเป็น 1 บรรยากาศ (atm) คำถามของเราคือ ความดันไอที่ 393 K คืออะไร? เรามีค่าอุณหภูมิสองค่าและค่าความดันหนึ่งค่า ดังนั้นเราจึงสามารถหาค่าความดันอื่นๆ โดยใช้สมการคลอสเซียส-คลาเปรอง โดยแทนค่าตัวแปรของเรา เราจะได้ ln(1/P2) = (ΔH_{ไอน้ำ}/R)((1/393) - (1/295)).
• โปรดทราบว่าสำหรับสมการ Clausius-Clapeyron คุณต้องใช้ค่าอุณหภูมิเสมอ เคลวิน. คุณสามารถใช้ค่าความดันใดๆ ก็ได้ตราบใดที่ค่าของ P1 และ P2 เท่ากัน

ขั้นตอนที่ 3 ป้อนค่าคงที่ของคุณ

สมการ Clausius-Clapeyron มีค่าคงที่สองค่า: R และ H_{ไอน้ำ}. R เท่ากับ 8.314 J/(K × Mol) เสมอ อย่างไรก็ตาม H_{ไอน้ำ} (เอนทาลปีของการกลายเป็นไอ) ขึ้นอยู่กับสารที่คุณต้องการความดันไอ ตามที่ระบุไว้ข้างต้น คุณสามารถหาค่าของ H. ได้_{ไอน้ำ} สำหรับสารต่างๆ ที่ด้านหลังหนังสือเรียนวิชาเคมีหรือฟิสิกส์ หรือออนไลน์ (เช่น ที่นี่)

• ในตัวอย่างของเรา สมมติว่าของเหลวของเราคือ น้ำบริสุทธิ์.

  ถ้าเราดูในตารางค่าของH_{ไอน้ำ}เราพบว่า H_{ไอน้ำ} น้ำบริสุทธิ์ประมาณ 40.65 KJ/โมล เนื่องจากค่า H ของเราอยู่ในหน่วยจูล ไม่ใช่กิโลจูล เราจึงสามารถแปลงเป็น 40,650 จูล/โมล

• แทนค่าคงที่เราจะได้ ln(1/P2) = (40,650/8, 314)((1/393) - (1/295)).

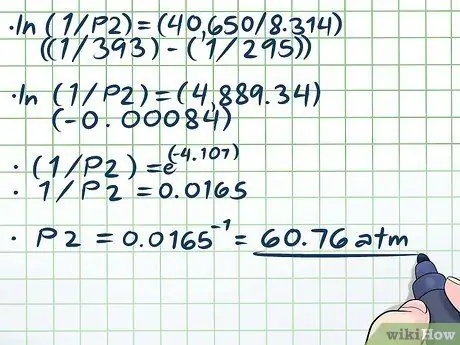
ขั้นตอนที่ 4 แก้สมการ

เมื่อคุณรวมตัวแปรทั้งหมดในสมการแล้ว ยกเว้นตัวแปรที่คุณต้องการ ให้ดำเนินการแก้สมการตามกฎของพีชคณิตธรรมดา

• ส่วนที่ยากเพียงอย่างเดียวในการแก้สมการของเรา (ln(1/P2) = (40,650/8, 314)((1/393) - (1/295))) กำลังแก้ไขล็อกธรรมชาติ (ln) ในการลบลอกธรรมชาติ ให้ใช้สมการทั้งสองข้างเป็นเลขชี้กำลังสำหรับค่าคงที่ทางคณิตศาสตร์ e กล่าวอีกนัยหนึ่ง ln(x) = 2 → e^ln(x) = อี² → x = อี².

• ทีนี้ มาแก้สมการของเรากัน:
• ln(1/P2) = (40,650/8, 314)((1/393) - (1/295))
• ln(1/P2) = (4889, 34)(-0, 00084)
• (1/P2) = e^{(-4, 107)}
• 1/P2 = 0.0165

• P2 = 0.0165^-1 = 60, 76 ตู้เอทีเอ็ม

  เรื่องนี้สมเหตุสมผล - ในภาชนะปิด การเพิ่มอุณหภูมิเกือบ 100 องศา (เหนือจุดเดือดเกือบ 20 องศา) จะผลิตไอน้ำจำนวนมาก เพิ่มความดันอย่างรวดเร็ว

วิธีที่ 2 จาก 3: การหาความดันไอด้วยสารละลายที่ละลายน้ำ

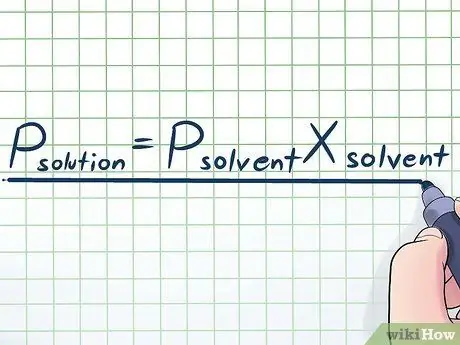
ขั้นตอนที่ 1 เขียนกฎของ Raoult

ในชีวิตจริง เราไม่ค่อยได้ทำงานกับของเหลวบริสุทธิ์ โดยปกติแล้ว เราทำงานกับของเหลวที่มีส่วนผสมของสารต่างๆ หลายชนิด สารผสมที่ใช้บ่อยที่สุดบางชนิดทำขึ้นโดยการละลายสารเคมีบางชนิดที่เรียกว่าตัวถูกละลายในสารเคมีจำนวนมากที่เรียกว่าตัวทำละลายเพื่อทำสารละลาย ในกรณีเหล่านี้ จะเป็นประโยชน์ที่จะทราบสมการที่เรียกว่ากฎของราอูลท์ (ตั้งชื่อตามนักฟิสิกส์ฟรองซัวส์-มารี ราอูลต์) ซึ่งเขียนดังนี้: NS_{ตัวละลาย}=ป_{ตัวทำละลาย}NS_{ตัวทำละลาย}. ในสูตรนี้ ตัวแปรแทน;

• NS_{ตัวละลาย}:

  แรงดันไอของสารละลายทั้งหมด (องค์ประกอบทั้งหมดรวมกัน)

• NS_{ตัวทำละลาย}:

  ความดันไอตัวทำละลาย

• NS_{ตัวทำละลาย}:

  เศษโมลของตัวทำละลาย

• อย่ากังวลหากคุณไม่ทราบคำศัพท์เช่นเศษส่วนโมล - เราจะอธิบายในขั้นตอนต่อไป

ขั้นตอนที่ 2 กำหนดตัวทำละลายและตัวถูกละลายในสารละลายของคุณ

ก่อนที่คุณจะคำนวณความดันไอของของเหลวผสม คุณต้องระบุสารที่คุณกำลังใช้ เพื่อเป็นการเตือนความจำ สารละลายจะเกิดขึ้นเมื่อตัวถูกละลายในตัวทำละลาย สารเคมีที่ละลายมักจะเรียกว่าตัวถูกละลาย และสารเคมีที่ทำให้ละลายมักจะเรียกว่าตัวทำละลาย

• มาลองใช้ตัวอย่างง่ายๆ ในส่วนนี้เพื่อแสดงแนวคิดที่เราพูดคุยกัน ตัวอย่างเช่น สมมติว่าเราต้องการหาความดันไอของน้ำเชื่อม ตามเนื้อผ้าน้ำเชื่อมเป็นน้ำตาลที่ละลายน้ำได้ (อัตราส่วน 1:1) ดังนั้นเราจึงสามารถพูดได้ว่า น้ำตาลคือตัวละลายของเรา และน้ำคือตัวทำละลายของเรา
• โปรดทราบว่าสูตรทางเคมีสำหรับซูโครส (น้ำตาลตาราง) คือ C₁₂ชม₂₂โอ₁₁. สูตรทางเคมีนี้จะมีความสำคัญมาก

ขั้นตอนที่ 3 ค้นหาอุณหภูมิของสารละลาย

ดังที่เราเห็นในหัวข้อ Clausius Clapeyron ด้านบน อุณหภูมิของของเหลวจะส่งผลต่อความดันไอ โดยทั่วไป ยิ่งอุณหภูมิสูงขึ้น ความดันไอก็จะยิ่งมากขึ้น - เมื่ออุณหภูมิสูงขึ้น ของเหลวก็จะระเหยกลายเป็นไอมากขึ้น ซึ่งจะทำให้ความดันในภาชนะเพิ่มขึ้น

ในตัวอย่างของเรา สมมติว่าอุณหภูมิของน้ำเชื่อม ณ จุดนี้คือ 298 K (ประมาณ 25 องศาเซลเซียส)

ขั้นตอนที่ 4 ค้นหาความดันไอของตัวทำละลาย

วัสดุอ้างอิงทางเคมีมักมีค่าความดันไอสำหรับสารและสารประกอบที่ใช้กันทั่วไปหลายชนิด แต่ค่าความดันเหล่านี้จะใช้ได้ก็ต่อเมื่อสารมีอุณหภูมิ 25 C/298 K หรือจุดเดือด หากสารละลายของคุณมีอุณหภูมิแบบใดแบบหนึ่ง คุณสามารถใช้ค่าอ้างอิงได้ แต่ถ้าไม่มี คุณจะต้องหาความดันไอที่อุณหภูมินั้น

• Clausius-Clapeyron ช่วยได้ - ใช้ความดันไออ้างอิงและ 298 K (25 C) สำหรับ P1 และ T1 ตามลำดับ
• ในตัวอย่างของเรา ส่วนผสมของเรามีอุณหภูมิ 25 C ดังนั้นเราจึงสามารถใช้ตารางอ้างอิงที่ง่ายของเราได้อย่างง่ายดาย เรารู้ว่าที่อุณหภูมิ 25 องศาเซลเซียส น้ำมีความดันไอเท่ากับ 23.8 มม. HG

ขั้นตอนที่ 5. ค้นหาเศษส่วนโมลของตัวทำละลายของคุณ

สิ่งสุดท้ายที่เราต้องทำก่อนจะแก้ปัญหานี้ได้คือ หาเศษส่วนโมลของตัวทำละลาย การหาเศษส่วนของโมลนั้นง่ายมาก เพียงแค่แปลงสารประกอบของคุณให้เป็นโมล จากนั้นให้หาเปอร์เซ็นต์ของสารประกอบแต่ละอย่างในจำนวนโมลทั้งหมดในสารนั้น กล่าวอีกนัยหนึ่ง เศษส่วนโมลของสารประกอบแต่ละชนิดเท่ากับ (โมลของสารประกอบ)/(จำนวนโมลในสารทั้งหมด).

• สมมติว่าสูตรของเราใช้น้ำเชื่อม น้ำ 1 ลิตร (L) และน้ำตาล 1 ลิตร (น้ำตาล)

  ในกรณีนี้เราต้องหาจำนวนโมลของสารประกอบแต่ละชนิด ในการทำเช่นนี้ เราจะหามวลของสารประกอบแต่ละชนิด จากนั้นใช้มวลโมลาร์ของสารแปลงให้เป็นโมล

• มวล (น้ำ 1 ลิตร): 1,000 กรัม (ก.)
• มวล (น้ำตาลทรายดิบ 1 ลิตร): ประมาณ 1,056, 8 ก
• โมล (น้ำ): 1,000 กรัม × 1 โมล/18.015 ก. = 55.51 โมล
• โมล (ซูโครส): 1,056, 7 กรัม × 1 โมล/342.2965 ก. = 3.08 โมล (โปรดทราบว่าคุณสามารถหามวลโมลาร์ของซูโครสได้จากสูตรทางเคมีของมันคือ C₁₂ชม₂₂โอ₁₁.)
• โมลทั้งหมด: 55.51 + 3.08 = 58.59 โมล
• เศษโมลของน้ำ: 55, 51/58, 59 = 0, 947

ขั้นตอนที่ 6. เสร็จสิ้น

สุดท้าย เรามีทุกอย่างที่จำเป็นในการแก้สมการกฎของราอูลท์ ส่วนนี้ง่ายมาก: เพียงเสียบค่าของคุณสำหรับตัวแปรในสมการกฎของราอูลท์แบบง่ายที่จุดเริ่มต้นของส่วนนี้ (NS_{ตัวละลาย} = ป_{ตัวทำละลาย}NS_{ตัวทำละลาย}).

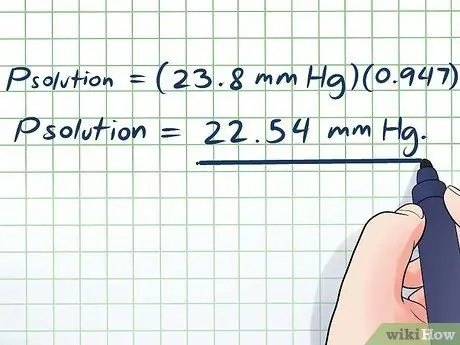
• เมื่อป้อนค่าของเรา เราได้รับ:
• NS_{สารละลาย} = (23.8 มม. ปรอท)(0, 947)

• NS_{สารละลาย} = 22.54 มม. ปรอท

  ผลลัพธ์นั้นสมเหตุสมผล - ในแง่ของโมล มีน้ำตาลน้อยมากที่ละลายในน้ำจำนวนมาก (แม้ว่าในโลกแห่งความเป็นจริง ส่วนผสมทั้งสองมีปริมาตรเท่ากัน) ดังนั้นความดันไอจึงลดลงเพียงเล็กน้อยเท่านั้น

วิธีที่ 3 จาก 3: การหาความดันไอในกรณีพิเศษ

ขั้นตอนที่ 1 ระวังอุณหภูมิและความดันมาตรฐาน

นักวิทยาศาสตร์มักใช้ชุดค่าอุณหภูมิและความดันเป็น "มาตรฐาน" ที่ใช้งานง่าย ค่าเหล่านี้เรียกว่าอุณหภูมิและความดันมาตรฐาน (หรือ STP) ปัญหาความดันไอมักอ้างถึงสภาวะ STP ดังนั้นจึงควรจำค่าเหล่านี้ไว้ ค่า STP ถูกกำหนดเป็น:

• อุณหภูมิ: 273, 15 K / 0 C / 32 F
• ความดัน: 760 มม. ปรอท / 1 ตู้เอทีเอ็ม / 101, 325 กิโลปาสกาล

ขั้นตอนที่ 2 จัดเรียงสมการของ Clausius-Clapeyron ใหม่เพื่อค้นหาตัวแปรอื่นๆ

ในตัวอย่างของเราในส่วนที่ 1 เราเห็นว่าสมการคลอเซียส–คลาเปยรอนมีประโยชน์มากในการค้นหาความดันไอของสารบริสุทธิ์ อย่างไรก็ตาม ไม่ใช่ทุกคำถามที่จะขอให้คุณค้นหา P1 หรือ P2 - หลายๆ คำถามจะขอให้คุณค้นหาค่าอุณหภูมิหรือบางครั้งแม้แต่ค่า H_{ไอน้ำ}. โชคดีที่ในกรณีเหล่านี้ การได้คำตอบที่ถูกต้องเป็นเพียงเรื่องของการจัดเรียงสมการใหม่ เพื่อให้ตัวแปรที่คุณต้องการแก้ถูกแยกจากด้านหนึ่งของเครื่องหมายเท่ากับ

• ตัวอย่างเช่น สมมติว่าเรามีของเหลวที่ไม่รู้จักซึ่งมีความดันไอ 25 ทอรร์ที่ 273 K และ 150 แรงบิดที่ 325 K และเราต้องการหาเอนทาลปีของการกลายเป็นไอของของเหลวนี้ (ΔH_{ไอน้ำ}). เราสามารถแก้ได้ดังนี้
• ln(P1/P2) = (ΔH_{ไอน้ำ}/R)((1/T2) - (1/T1))
• (ln(P1/P2))/((1/T2) - (1/T1)) = (ΔH_{ไอน้ำ}/NS)
• R × (ln(P1/P2))/((1/T2) - (1/T1)) = H_{ไอน้ำ} ตอนนี้เราป้อนค่าของเรา:
• 8, 314 J/(K × โมล) × (-1, 79)/(-0, 00059) = H_{ไอน้ำ}
• 8, 314 J/(K × โมล) × 3,033, 90 = H_{ไอน้ำ} = 25,223, 83 J/โมล

ขั้นตอนที่ 3 คำนวณความดันไอของตัวถูกละลายเมื่อสารผลิตไอ

ในตัวอย่างกฎ Raoult ด้านบน ตัวถูกละลาย น้ำตาล ของเราไม่มีแรงกดใดๆ ในตัวมันเองที่อุณหภูมิปกติ (ลองคิดดูว่า ครั้งสุดท้ายที่คุณเห็นน้ำตาลหนึ่งชามระเหยในตู้บนของคุณคือเมื่อใด) อย่างไรก็ตาม เมื่อตัวละลายของคุณทำ ระเหย ซึ่งจะส่งผลต่อความดันไอของคุณ เราพิจารณาสิ่งนี้โดยใช้สมการกฎของราอูลต์ที่แก้ไขแล้ว: NS_{สารละลาย} = (ป_{สารประกอบ}NS_{สารประกอบ}) สัญลักษณ์ซิกม่า (Σ) หมายความว่าเราจำเป็นต้องบวกแรงดันไอทั้งหมดของสารประกอบต่างๆ เพื่อให้ได้คำตอบ

• ตัวอย่างเช่น สมมติว่าเรามีสารละลายที่ทำจากสารเคมีสองชนิด ได้แก่ เบนซีนและโทลูอีน ปริมาตรรวมของสารละลายคือ 12 มิลลิลิตร (มล.) เบนซิน 60 มล. และโทลูอีน 60 มล. อุณหภูมิของสารละลายคือ 25°C และความดันไอของสารเคมีแต่ละชนิดที่ 25°C คือ 95.1 มม.ปรอท สำหรับน้ำมันเบนซิน และ 28.4 มม.ปรอท สำหรับโทลูอีน ด้วยค่าเหล่านี้ ให้หาความดันไอของสารละลาย เราสามารถทำได้ดังนี้โดยใช้ค่าความหนาแน่นมาตรฐาน มวลโมลาร์ และความดันไอสำหรับสารเคมีทั้งสองของเรา:
• มวล (เบนซิน): 60 มล. = 0.060 ลิตร &ครั้ง 876.50 กก./1,000 ลิตร = 0.053 กก. = 53 กรัม
• มวล (โทลูอีน): 0.060 L &ครั้ง 866, 90 kg/1,000 L = 0.052 kg = 52 กรัม
• โมล (เบนซิน): 53 ก. × 1 โมล/78, 11 ก. = 0.679 โมล
• โมล (โทลูอีน): 52 ก. × 1 โมล/92, 14 ก. = 0.564 โมล
• จำนวนโมลทั้งหมด: 0.679 + 0.564 = 1.243
• เศษส่วนโมล (เบนซิน): 0.679/1, 243 = 0.546
• เศษโมล (โทลูอีน): 0.564/1, 243 = 0.454
• วิธีแก้ปัญหา: P_{สารละลาย} = ป_{เบนซิน}NS_{เบนซิน} + พี่_{โทลูอีน}NS_{โทลูอีน}
• NS_{สารละลาย} = (95.1 มม. ปรอท)(0, 546) + (28.4 มม. ปรอท)(0, 454)
• NS_{สารละลาย} = 51.92 มม. ปรอท + 12.89 มม. ปรอท = 64, 81 มม. ปรอท

เคล็ดลับ

• ในการใช้สมการ Clausius Clapeyron ข้างต้น ต้องวัดอุณหภูมิเป็นเคลวิน (เขียนเป็น K) หากคุณมีอุณหภูมิเป็นเซลเซียส คุณต้องแปลงโดยใช้สูตรต่อไปนี้: NS_k = 273 + T_ค
• สามารถใช้วิธีการข้างต้นได้เนื่องจากพลังงานเป็นสัดส่วนกับปริมาณความร้อนที่ใช้ อุณหภูมิของของเหลวเป็นเพียงปัจจัยแวดล้อมเดียวที่ส่งผลต่อความดันไอ