- ผู้เขียน Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:42.
- แก้ไขล่าสุด 2025-01-23 12:49.
รูปร่างแบนมีรูปทรงต่างๆ มากมาย และมีเหตุผลหลายประการที่คุณอาจต้องการคำนวณพื้นที่ ตั้งแต่ทำการบ้านไปจนถึงการประเมินว่าต้องใช้สีมากเพียงใดในการทาสีห้องนั่งเล่นใหม่ ไม่ต้องกังวล wikiHow มีคำตอบ! เริ่มจากขั้นตอนที่ 1 ด้านล่างเพื่อทราบวิธีการคำนวณพื้นที่ของตัวเลขระนาบ
ขั้นตอน
วิธีที่ 1 จาก 7: สี่เหลี่ยมจัตุรัส สี่เหลี่ยมผืนผ้า และสี่เหลี่ยมด้านขนาน
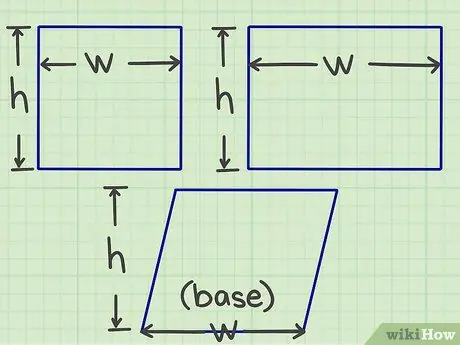
ขั้นตอนที่ 1. วัดความยาวและความกว้าง
เริ่มวัดหรือหาความยาวและความกว้างของรูปทรงแบน (หรืออีกนัยหนึ่งคือขนาดของแต่ละด้านที่พบกันที่จุดเดียว)
- สำหรับสี่เหลี่ยมด้านขนาน คุณต้องหาฐานและความสูง แต่พูดง่ายๆ ก็คือ แนวคิดจะเหมือนกับความยาวและความกว้าง
- ในโลกแห่งความเป็นจริง คุณอาจต้องวัดผลด้วยตัวเอง แต่เมื่อทำการบ้าน ครูมักจะจดตัวเลขไว้พร้อมกับรูปภาพของรูปทรงนั้นแล้ว
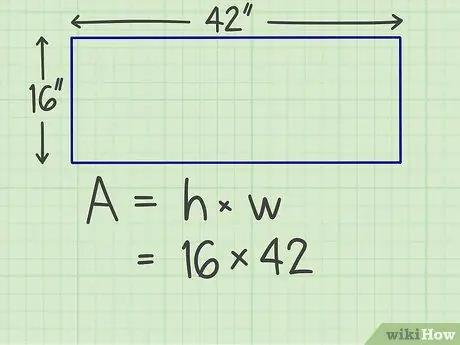
ขั้นตอนที่ 2 คูณด้าน
คูณด้านหนึ่งด้วยอีกด้านหนึ่ง ตัวอย่างเช่น สมมติว่าคุณมีสี่เหลี่ยมผืนผ้าที่มีความกว้าง 16 นิ้วและความยาว 42 นิ้ว ดังนั้นคุณต้องคำนวณ 16 x 42
หากคุณกำลังคำนวณพื้นที่ของสี่เหลี่ยมจัตุรัส (เดิมคือสี่เหลี่ยมจัตุรัส) ประหยัดเวลาด้วยการยกกำลังสองด้านใดด้านหนึ่งโดยใช้เครื่องคิดเลข หากด้านข้างมีขนาด 4 ม. ให้กดปุ่ม 4 แล้วกดปุ่มสี่เหลี่ยมบนเครื่องคิดเลขเพื่อแสดงผลลัพธ์ สแควร์หมายถึงการคูณตัวเลขด้วยตัวมันเอง
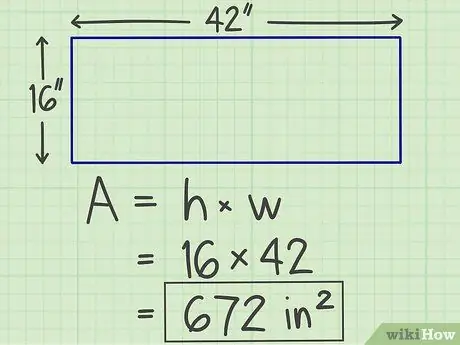
ขั้นตอนที่ 3 เขียนผลลัพธ์
การคูณที่คุณทำก่อนหน้านี้จะสร้างตัวเลข ซึ่งเป็นพื้นที่ของระนาบที่คุณกำลังคำนวณ โดยมีหน่วย "กำลังสอง" ดังนั้นสี่เหลี่ยมผืนผ้าที่เราคำนวณไว้ก่อนหน้านี้จึงมีพื้นที่ 672 ตารางนิ้ว
บางครั้งหน่วยสี่เหลี่ยมจัตุรัสนี้ก็เขียนด้วยเลข 2 เล็ก ๆ ที่เพิ่มขึ้นเล็กน้อยหลังชื่อหน่วย (เช่น พลังการเขียน)
วิธีที่ 2 จาก 7: สี่เหลี่ยมคางหมู
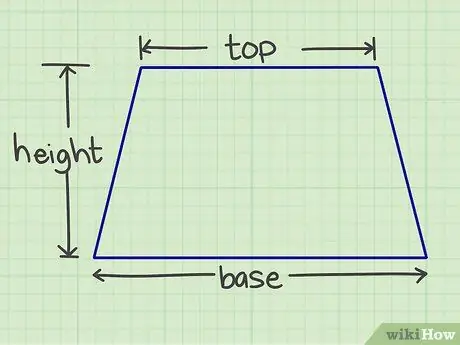
ขั้นตอนที่ 1 วัดจำนวนที่ต้องการ
คุณจะต้องวัดฐาน หลังคา และความสูง ฐานและหลังคาเป็นด้านขนานกัน ในขณะที่ความสูงเป็นเส้นตั้งฉากที่เชื่อมด้านขนานทั้งสองเข้าด้วยกัน
ในโลกแห่งความเป็นจริง คุณอาจต้องวัดผลด้วยตัวเอง แต่เมื่อทำการบ้าน ครูมักจะจดตัวเลขไว้พร้อมกับรูปภาพของรูปทรงนั้นแล้ว
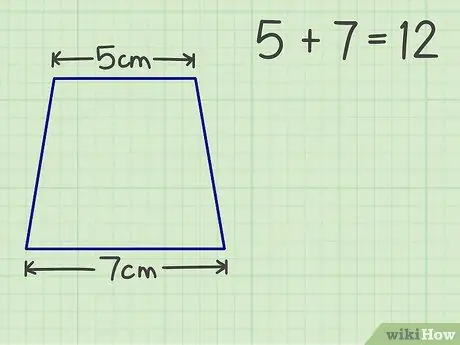
ขั้นตอนที่ 2 เพิ่มด้านขนานทั้งสองข้าง
ตัวอย่างเช่น สี่เหลี่ยมคางหมูของเรามีหลังคา 5 ซม. และฐาน 7 ซม. ผลรวมของด้านคู่ขนานทั้งสองข้างคือ 12
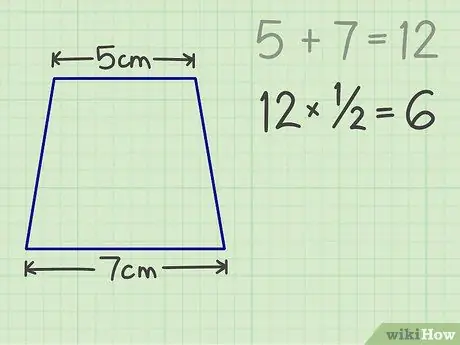
ขั้นตอนที่ 3 คูณตัวเลขด้วย 1/2 ผลลัพธ์คือ 6
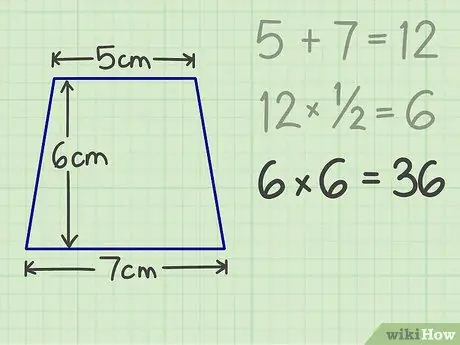
ขั้นตอนที่ 4 หลังจากนั้นให้คูณผลลัพธ์ด้วยความสูง
ตัวอย่างเช่น หากสี่เหลี่ยมคางหมูมีความสูง 6 ซม. ผลลัพธ์สุดท้ายคือ 36
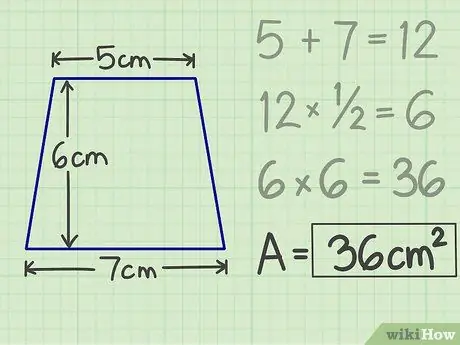
ขั้นตอนที่ 5. เขียนผลลัพธ์
การคูณที่คุณทำก่อนหน้านี้จะสร้างตัวเลข กล่าวคือ พื้นที่ของสี่เหลี่ยมคางหมู ดังนั้นสำหรับสี่เหลี่ยมคางหมูที่มีหลังคาสูง 5 ซม. ฐาน 7 ซม. และสูง 6 ซม. พื้นที่คือ 36 ซม. ตร.ม.
วิธีที่ 3 จาก 7: วงกลม
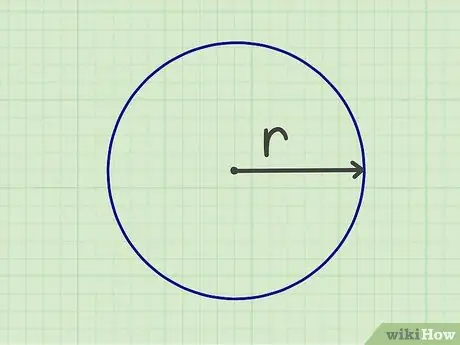
ขั้นตอนที่ 1. วัดรัศมี
เพื่อให้สามารถคำนวณพื้นที่ของวงกลมได้ คุณต้องวัดรัศมี รัศมีคือระยะทางจากจุดศูนย์กลางของวงกลมถึงขอบ คุณยังสามารถวัดรัศมีโดยการวัดเส้นผ่านศูนย์กลาง (ความกว้างของวงกลมจากขอบหนึ่งไปอีกขอบหนึ่ง) แล้วหารตัวเลขด้วยสอง
ในโลกแห่งความเป็นจริง คุณอาจต้องวัดผลด้วยตัวเอง แต่เมื่อทำการบ้าน ครูมักจะจดตัวเลขไว้พร้อมกับรูปภาพของรูปทรงนั้นแล้ว
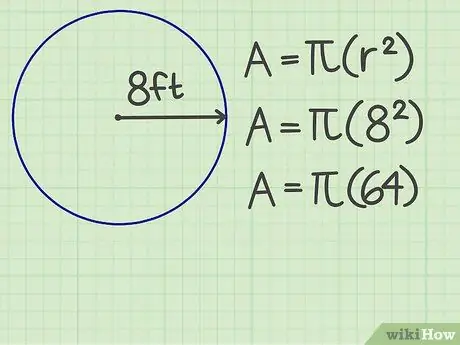
ขั้นตอนที่ 2. ยกนิ้วให้
คูณจำนวนรัศมีด้วยตัวมันเอง ตัวอย่างเช่น รัศมีของวงกลมเท่ากับ 8 ฟุต ผลลัพธ์ที่ได้คือ 64
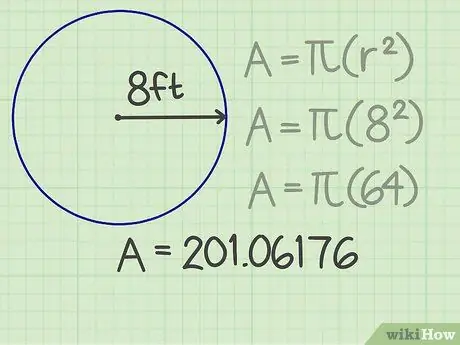
ขั้นตอนที่ 3 คูณผลลัพธ์ด้วย pi
Pi (π) เป็นตัวเลขสำคัญที่ใช้ในสูตรต่างๆ หากคุณกำลังใช้เครื่องคิดเลข ให้กดปุ่ม pi เพื่อให้ได้ผลลัพธ์ที่แม่นยำ มิฉะนั้น เพื่อให้การคำนวณของคุณง่ายขึ้น คุณสามารถปัดเศษ pi เป็นสองสามหลักหลังเครื่องหมายจุลภาค เช่น 3, 14159 เมื่อคุณคูณตัวเลขนี้ด้วยกำลังสองของรัศมี ผลลัพธ์จะเป็น 201, 06176
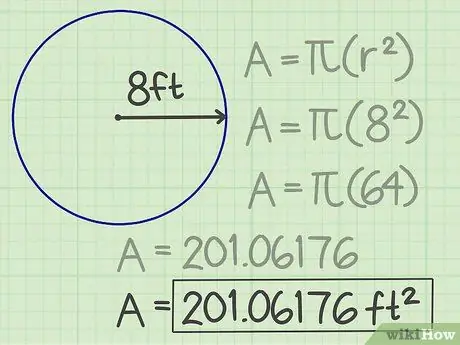
ขั้นตอนที่ 4 เขียนผลลัพธ์
จำนวนที่ได้รับ 201, 06176 คือพื้นที่ของวงกลม ดังนั้นพื้นที่ของมันคือ 201,06176 ตารางฟุต
วิธีที่ 4 จาก 7: ภาคส่วน (Juring)
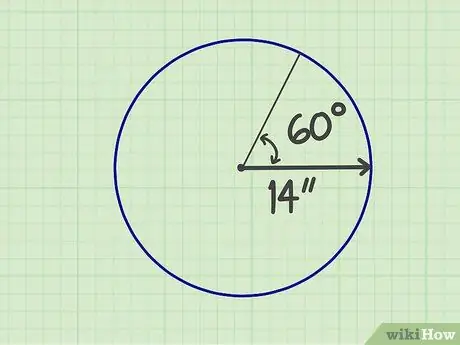
ขั้นตอนที่ 1 วัดจำนวนที่ต้องการ
เซกเตอร์คือส่วนของวงกลมที่เกิดจากรัศมีสองรัศมีและขอบ เพื่อให้รูปร่างเหมือนพัด คุณต้องรู้ขนาดของรัศมีและมุมที่ประกอบเป็น "พัดลม" ตัวอย่างเช่น สมมติว่าเซกเตอร์มีรัศมี 14 นิ้วและมีมุม 60 องศา
ในโลกแห่งความเป็นจริง คุณอาจต้องวัดผลด้วยตัวเอง แต่เมื่อทำการบ้าน ครูมักจะจดตัวเลขไว้พร้อมกับรูปภาพของรูปทรงนั้นแล้ว
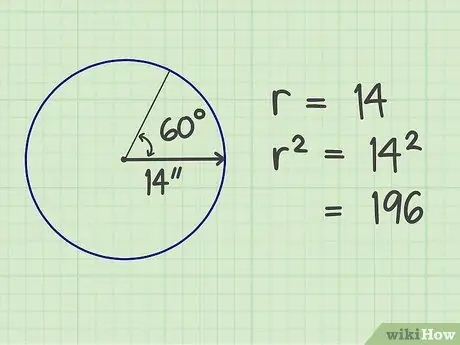
ขั้นตอนที่ 2. ยกนิ้วให้
คูณจำนวนรัศมีด้วยตัวมันเอง ผลลัพธ์คือ 196 (14x14)

ขั้นตอนที่ 3 คูณผลลัพธ์ด้วย pi
Pi (π) เป็นตัวเลขสำคัญที่ใช้ในสูตรต่างๆ หากคุณกำลังใช้เครื่องคิดเลข ให้กดปุ่ม pi เพื่อให้ได้ผลลัพธ์ที่แม่นยำ มิฉะนั้น เพื่อให้การคำนวณของคุณง่ายขึ้น คุณสามารถปัดเศษ pi เป็นสองสามหลักหลังเครื่องหมายจุลภาค เช่น 3, 14159 หากคุณคูณตัวเลขนี้ด้วยกำลังสองของรัศมี ผลลัพธ์จะเป็น 615, 75164

ขั้นตอนที่ 4 แบ่งการวัดมุมด้วย 360
แบ่งมุมพัดลมเซกเตอร์ด้วย 360 (การวัดมุมของวงกลมเต็ม) จากตัวอย่างด้านบน ผลลัพธ์จะอยู่ที่ประมาณ 0.166 หากคุณคำนวณด้วยเครื่องคิดเลข ผลลัพธ์จะยาวกว่าและทำซ้ำจริง ๆ แต่ในที่นี้จะมีการปัดเศษเพื่อให้การคำนวณง่ายขึ้น

ขั้นตอนที่ 5. คูณตัวเลขนี้ด้วยตัวเลขก่อนหน้า
คูณจำนวนที่คุณได้รับหลังจากคุณหารมุมด้วย 360 ด้วยจำนวนที่คุณได้รับก่อนหน้านี้หลังจากคูณ pi ด้วยกำลังสองของรัศมี จากตัวอย่างข้างต้น ผลลัพธ์คือ 102, 214 (หลังปัดเศษ)
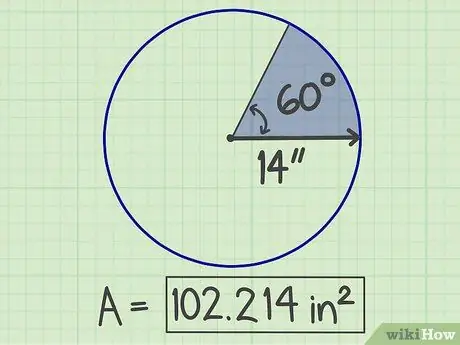
ขั้นตอนที่ 6. เขียนผลลัพธ์
ตัวเลขที่ได้คือพื้นที่ของเซกเตอร์ซึ่งเท่ากับ 102, 214 ตารางนิ้ว
วิธีที่ 5 จาก 7: วงรี
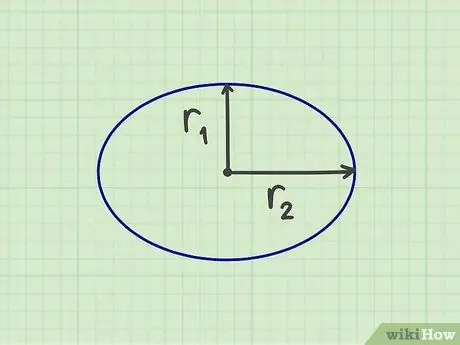
ขั้นตอนที่ 1 วัดจำนวนที่ต้องการ
ในการคำนวณพื้นที่ของวงรี คุณต้องวัด "รัศมี" สองอัน กล่าวคือ รัศมีสั้นและรัศมียาว ซึ่งเท่ากับความกว้างครึ่งหนึ่งและความสูงของวงรีครึ่งหนึ่ง คุณยังสามารถวัดรัศมีสั้นจากจุดศูนย์กลางของวงรีไปยังด้านที่สั้นที่สุด และรัศมียาวจากจุดศูนย์กลางของวงรีไปยังด้านที่ยาวที่สุดได้ รัศมีสั้นควรสร้างมุมฉากกับรัศมียาว
ในโลกแห่งความเป็นจริง คุณอาจต้องวัดผลด้วยตัวเอง แต่เมื่อทำการบ้าน ครูมักจะจดตัวเลขไว้พร้อมกับรูปภาพของรูปทรงนั้นแล้ว
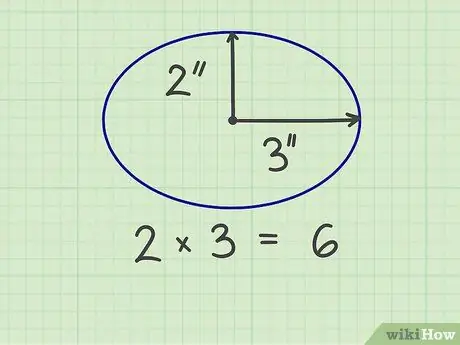
ขั้นตอนที่ 2 คูณสองนิ้ว
ตัวอย่างเช่น วงรีกว้าง 6 นิ้วและสูง 4 นิ้ว ดังนั้นรัศมีคือ 3 นิ้วและ 2 นิ้ว เมื่อนำตัวเลขทั้งสองมาคูณกัน ผลลัพธ์จะเป็น 6 (3 x 2)

ขั้นตอนที่ 3 คูณผลลัพธ์ด้วย pi
Pi (π) เป็นตัวเลขสำคัญที่ใช้ในสูตรต่างๆ หากคุณกำลังใช้เครื่องคิดเลข ให้กดปุ่ม pi เพื่อให้ได้ผลลัพธ์ที่แม่นยำ มิฉะนั้น เพื่อให้การคำนวณของคุณง่ายขึ้น คุณสามารถปัดเศษ pi เป็นสองสามหลักหลังเครื่องหมายจุลภาค เช่น 3, 14159 เมื่อคุณคูณตัวเลขนี้ด้วยกำลังสองของรัศมี ผลลัพธ์จะเป็น 18, 84954
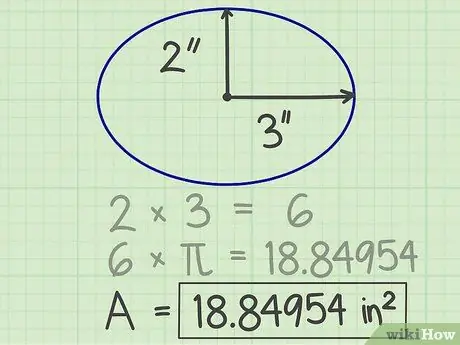
ขั้นตอนที่ 4 เขียนผลลัพธ์
ตัวเลขที่ได้จากการคำนวณข้างต้นคือพื้นที่ของวงรี ในตัวอย่างข้างต้น พื้นที่ของวงรีคือ 18.84954 ตารางนิ้ว
วิธีที่ 6 จาก 7: สามเหลี่ยม
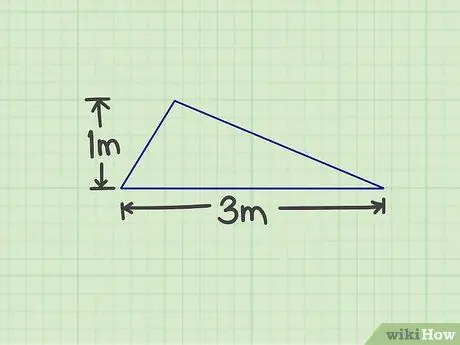
ขั้นตอนที่ 1 วัดจำนวนที่ต้องการ
คุณต้องวัดฐานและความสูงของสามเหลี่ยม ด้านใดของสามเหลี่ยมสามารถเป็นฐานได้ ตราบใดที่คุณสามารถวัดความสูงได้ ตัวอย่างเช่น มีรูปสามเหลี่ยมที่มีฐาน 3 ม. และสูง 1 ม.
ในโลกแห่งความเป็นจริง คุณอาจต้องวัดผลด้วยตัวเอง แต่เมื่อทำการบ้าน ครูมักจะจดตัวเลขไว้พร้อมกับรูปภาพของรูปทรงนั้นแล้ว
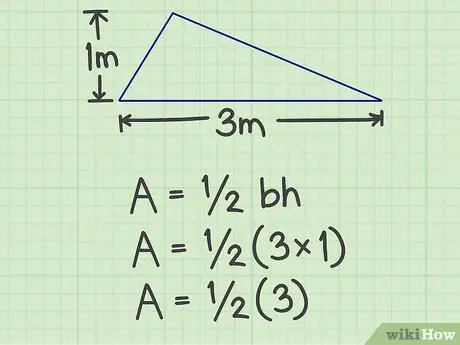
ขั้นตอนที่ 2 คูณฐานด้วยความสูง
จากตัวอย่างข้างต้น ผลลัพธ์คือ 3 (3x1)
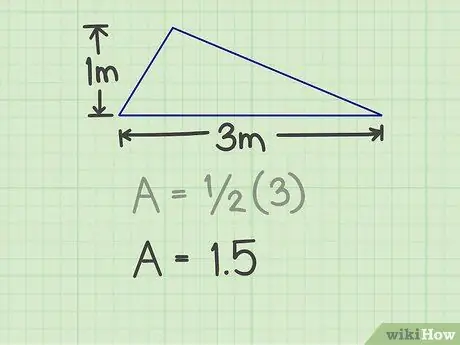
ขั้นตอนที่ 3 คูณผลลัพธ์ด้วย 1/2
การคูณนี้จะได้เลข 1, 5
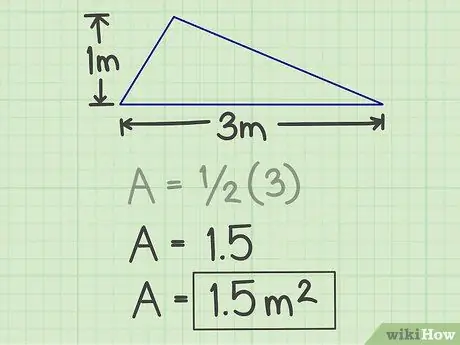
ขั้นตอนที่ 4 เขียนผลลัพธ์
ตัวเลขที่สร้างจากการคำนวณข้างต้นคือพื้นที่ของสามเหลี่ยม และจากตัวอย่างด้านบน พื้นที่ของมันคือ 1.5 ตารางเมตร
วิธีที่ 7 จาก 7: Complex Flat Build
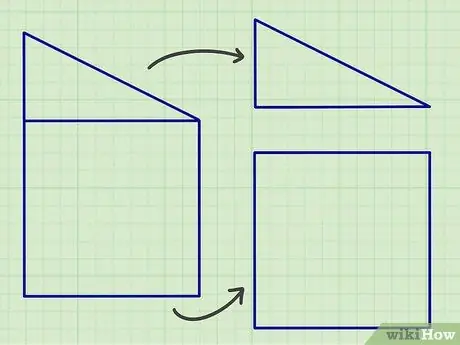
ขั้นตอนที่ 1 แยกรูปร่างระนาบที่ซับซ้อนออกเป็นส่วน ๆ ซึ่งประกอบด้วยรูปทรงเรขาคณิตมาตรฐานด้านบน
หากสิ่งที่คุณกำลังทำคือการบ้าน การแบ่งรูปร่างที่ซับซ้อนออกเป็นรูปแบนที่กล่าวถึงก่อนหน้านี้อาจเป็นเรื่องง่าย แต่ในโลกแห่งความเป็นจริง คุณอาจต้องแบ่งรูปทรงแบนเป็นรูปทรงแบนหลายๆ อันเพื่อให้ได้ผลการคำนวณที่แม่นยำ.
วิธีที่ดีในการเริ่มต้นคือการมองหาเส้นที่ขนานกันหรืออยู่ในมุมที่กำหนด เนื่องจากรูปร่างแบนๆ ส่วนใหญ่จะประกอบขึ้นจากรูปทรงเหล่านี้
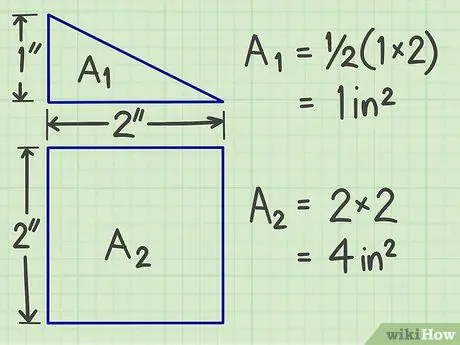
ขั้นตอนที่ 2 คำนวณพื้นที่สำหรับตัวเลขระนาบแต่ละอันที่เกิดจากการแยกตัว
ใช้วิธีการด้านบนเพื่อให้ได้พื้นที่ของรูปทรงแบนแต่ละอัน
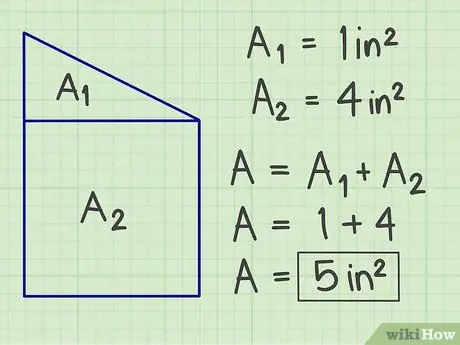
ขั้นตอนที่ 3 เพิ่มผลลัพธ์
รวมพื้นที่ที่คำนวณได้ทั้งหมดเพื่อให้ได้พื้นที่ทั้งหมดของรูประนาบเชิงซ้อนของคุณ
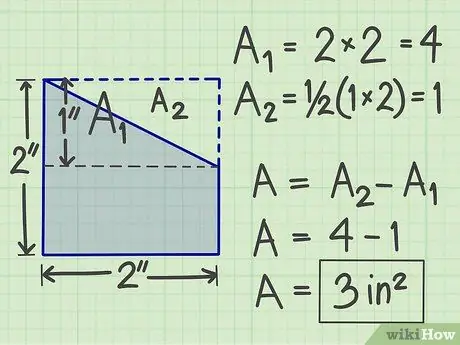
ขั้นตอนที่ 4 ใช้วิธีการอื่น
มีหลายวิธีที่คุณสามารถลองได้ ขึ้นอยู่กับรูปร่างของรูปร่างแบนที่ซับซ้อน ตัวอย่างเช่น คุณสามารถเพิ่มรูปร่างระนาบจินตภาพเพื่อให้มันกลายเป็นรูปร่างระนาบเรขาคณิตมาตรฐานได้ หลังจากนั้นให้คำนวณพื้นที่แล้วลบพื้นที่ของรูปทรงแบนจินตภาพที่คุณเคยบวก
เคล็ดลับ
- ใช้เครื่องคิดเลขนี้หากคุณต้องการความช่วยเหลือในการแก้ปัญหาการคำนวณทางคณิตศาสตร์
- ขอความช่วยเหลือจากเพื่อนหากคุณยังคงประสบปัญหา!
คำเตือน
- จะดีกว่าเสมอที่จะตรวจสอบผลการคำนวณซ้ำเพื่อให้แน่ใจว่าถูกต้อง!
- ตรวจสอบให้แน่ใจว่าหน่วยที่คุณใช้นั้นเหมือนกันทั้งหมด (ซม. ม. นิ้ว ฯลฯ) เมื่อทำการคำนวณ ดังนั้นคุณจะไม่ได้รับการคำนวณผิดพลาดเนื่องจากหน่วยผสม!

