- ผู้เขียน Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- แก้ไขล่าสุด 2025-01-23 12:49.
ลูกบิลเลียดตีกันด้วยความยืดหยุ่นที่สมบูรณ์แบบ กล่าวคือ พลังงานจลน์ของการเคลื่อนไหวเกือบจะถูกรักษาไว้เกือบหมด และพลังงานจลน์น้อยมากที่จะถูกแปลงเป็นความร้อนหรือพลังงานอื่น ทำให้บิลเลียดเป็นกีฬาที่น่าสนใจสำหรับการวิเคราะห์ทางคณิตศาสตร์ หากคุณควบคุมวิธีที่จะจิ้มลูกบอลสีขาวได้อย่างสมบูรณ์และไปที่ใด คุณจะสามารถคาดเดาได้เสมอว่าจะเกิดอะไรขึ้น
ขั้นตอน
ส่วนที่ 1 จาก 3: การทำนายมุมการเด้งของลูกบอลบนราง
ขั้นตอนที่ 1 เข้าใจกฎแห่งการสะท้อน
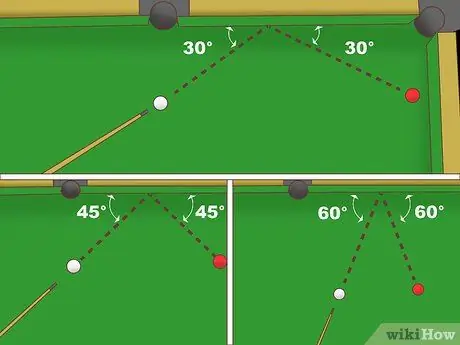
ผู้เล่นพูลหลายคนรู้คณิตศาสตร์ง่ายๆ นี้อยู่แล้วเพราะจำเป็นทุกครั้งที่ต้องการตีกลับลูกบอลบนราง (ขอบเบาะบนโต๊ะพูล) กฎข้อนี้ระบุว่ามุมตกกระทบของการสะท้อนเท่ากับมุมออก กล่าวคือ หากลูกบอลกระทบรางที่มุม 30º มุมสะท้อนกลับจะเป็น 30º ด้วย
กฎการสะท้อนเดิมอ้างถึงธรรมชาติของแสง โดยปกติ กฎข้อนี้จะอ่านว่า "มุมตกกระทบเท่ากับมุมสะท้อน"
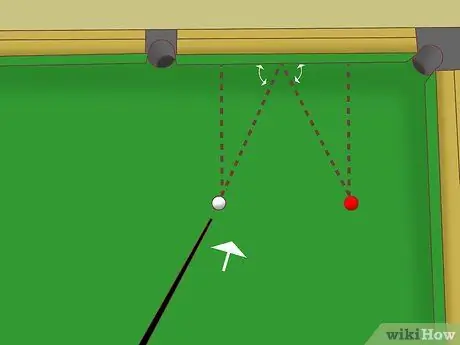
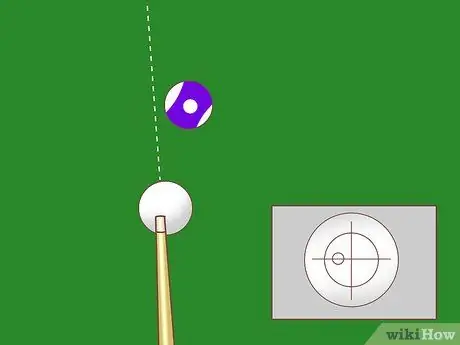
ขั้นตอนที่ 2. ตั้งลูกบอลสีขาวและลูกบอลวัตถุให้ห่างจากรางเท่ากัน
ในสถานการณ์นี้ เป้าหมายของคุณคือการกระเด้งลูกบอลสีขาวบนรางและตีลูกบอลวัตถุ ตอนนี้ ลองใช้เทคนิคเรขาคณิตพื้นฐานต่อไปนี้:
- ลากเส้นเงาจากลูกบอลสีขาวซึ่งตั้งฉากกับราง นี่คือบรรทัดแรก
- จากนั้น ให้จินตนาการถึงเส้นทางของการสะท้อนของลูกบอลสีขาวไปยังรางรถไฟ เส้นนี้คือด้านตรงข้ามมุมฉาก (ด้านตรงข้ามมุมฉาก) ของสามเหลี่ยมมุมฉากที่เกิดจากเส้นแรกและราง
- ลองนึกภาพว่าลูกบอลสีขาวกระเด้งออกจากรางและกระทบกับลูกบอลวัตถุ สมมติว่ามีสามเหลี่ยมมุมฉากที่สองบนทรงกลมของวัตถุที่สมมาตรกับสามเหลี่ยมแรก
ขั้นตอนที่ 3 พิสูจน์ว่าสามเหลี่ยมทั้งสองนี้เท่ากัน
ในกรณีนี้ เราสามารถใช้กฎ "มุมด้านข้าง" ได้ หากสามเหลี่ยมทั้งสองมีมุมเท่ากันสองมุม และด้านหนึ่งเหมือนกัน (ในรูปแบบเดียวกัน) แสดงว่าสามเหลี่ยมสองรูปนั้นเท่ากัน (กล่าวคือรูปร่างและขนาดเหมือนกัน) เราสามารถพิสูจน์ได้ว่าสามเหลี่ยมสองรูปนี้บนโต๊ะพูลเป็นไปตามเงื่อนไขเหล่านี้หรือไม่:
- กฎการสะท้อนกล่าวว่ามุมสองมุมระหว่างด้านตรงข้ามมุมฉากกับรางมีขนาดเท่ากัน
- ทั้งสองเป็นมุมฉาก ดังนั้นแต่ละมุมจึงมีมุม 90º
- เนื่องจากลูกบอลทั้งสองลูกอยู่ห่างจากรางเท่ากัน ทั้งสองด้านระหว่างลูกบอลกับรางจึงมีความยาวเท่ากัน
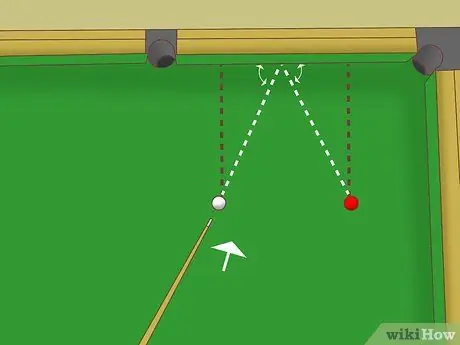
ขั้นตอนที่ 4. เล็งไปที่จุดกึ่งกลางของราง
เนื่องจากสามเหลี่ยมสองรูปนี้เท่ากัน ความยาวของด้านบนรางจึงเท่ากัน นั่นคือระยะทางจากจุดกระดอนไปยังลูกบอลทั้งสองจะเท่ากัน เล็งไปที่จุดกึ่งกลางหากลูกบอลสีขาวและลูกบอลวัตถุอยู่ห่างจากรางเท่ากัน
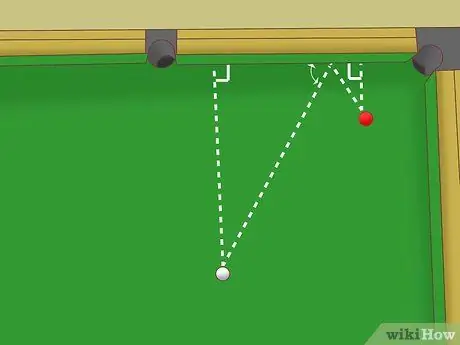
ขั้นตอนที่ 5. ใช้รูปสามเหลี่ยมที่คล้ายกันหากลูกบอลสีขาวและลูกบอลวัตถุอยู่ห่างจากรางไม่เท่ากัน
ระยะทางของลูกบอลสีขาวไปยังรางรถไฟเป็นสองเท่าของระยะทางของลูกบอลวัตถุไปยังราง คุณยังสามารถจินตนาการถึงสามเหลี่ยมมุมฉากสองรูปที่เกิดจากเส้นทางในอุดมคติของทรงกลมสีขาว และใช้สัญชาตญาณทางเรขาคณิตของคุณเพื่อเล็ง:
- สามเหลี่ยมสองรูปยังมีมุมเท่ากัน แต่ด้านยาวต่างกัน นั่นคือ สามเหลี่ยมสองรูปยังคงคล้ายกัน: รูปร่างเหมือนกัน แต่ขนาดต่างกัน
- เนื่องจากลูกบอลสีขาวอยู่ห่างจากรางเป็นสองเท่า สามเหลี่ยมแรกจึงมีขนาดใหญ่เป็นสองเท่าของสามเหลี่ยมที่สอง
- นั่นคือ ด้านรางของสามเหลี่ยมแรกจะยาวเป็นสองเท่าของด้านรางของสามเหลี่ยมที่สอง
- ในกรณีนี้ ให้เล็งไปที่จุดบนรางที่ระยะห่างจากลูกบอลวัตถุ เพราะ เป็นสองเท่า.
ส่วนที่ 2 จาก 3: การคำนวณมุมของการกระแทกของวัตถุลูก
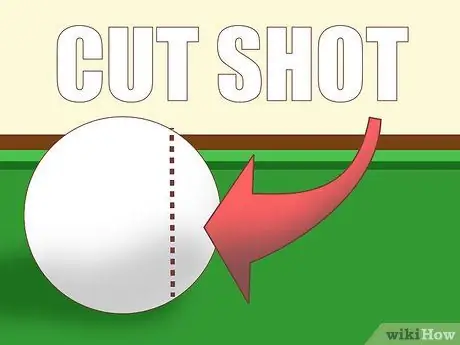
ขั้นตอนที่ 1 เรียนรู้พื้นฐาน
การเล่นบิลเลียดส่วนใหญ่เป็นลูกเตะมุมหรือ "การกรีด" ซึ่งหมายความว่าลูกบอลสีขาวจะไม่กระทบกับวัตถุโดยตรง ยิ่งลูกบอลกระทบ "ทินเนอร์" มากเท่าใด มุมของเส้นทางลูกของวัตถุก็จะยิ่งมากขึ้นเท่านั้น ขึ้นอยู่กับวิถีโคจรของลูกบอลสีขาว
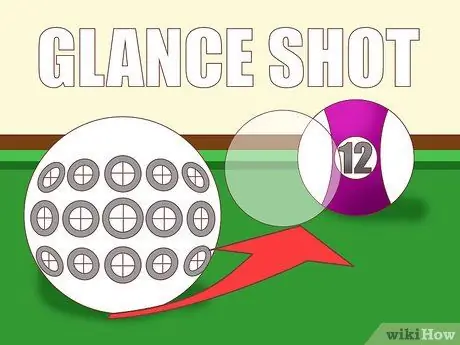
ขั้นตอนที่ 2 ประเมินความสมบูรณ์ของผลกระทบ
วิธีที่ดีในการประเมินผลกระทบนี้คือการตรวจสอบผลกระทบกับวิถีโคจรที่วางแผนไว้ของลูกบอล เมื่อลูกบอลชนกัน ลูกบอลสีขาว "ทับซ้อน" บนลูกบอลวัตถุจากมุมมองของคุณมากแค่ไหน? คำตอบจะแสดงให้เห็นว่า "เต็ม" ลูกบอลได้อย่างไร:
- ตายบนทับซ้อนกันอย่างสมบูรณ์ คุณสามารถพูดระดับของ "ความสมบูรณ์" คือ 1
- หากลูกบอลสีขาวคลุมลูกบอลของวัตถุ แสดงว่าลูกบอลชนกันเต็ม
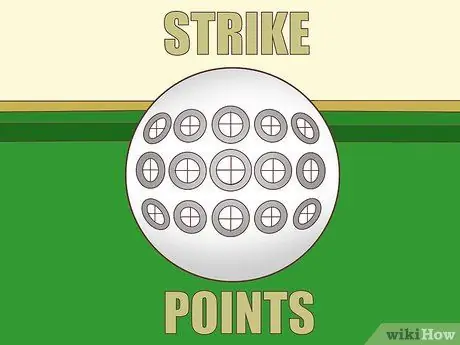
ขั้นตอนที่ 3 ประเมินมุมตามระดับความแน่น
กราฟของปริมาณทั้งสองนี้ไม่ได้เป็นเส้นตรง แต่ใกล้พอที่คุณจะประมาณได้โดยการเพิ่ม 15º ทุกครั้งที่คุณลบความสมบูรณ์ มิฉะนั้น คุณสามารถใช้การวัดต่อไปนี้ซึ่งมีความแม่นยำมากขึ้น:
- การกระแทกโดยตรง (ระดับความแน่นที่ 1) ส่งผลให้มุมตัด 0º ลูกบอลวัตถุจะดำเนินต่อไปตามเส้นทางของลูกบอลสีขาว
- การกระแทกเต็มที่จะส่งลูกบอลวัตถุไปที่มุม 14.5º
- การกระแทกเต็มที่จะส่งลูกบอลวัตถุไปที่มุม30º
- การชนกันเต็มที่จะส่งลูกบอลวัตถุไปที่มุม 48, 6º
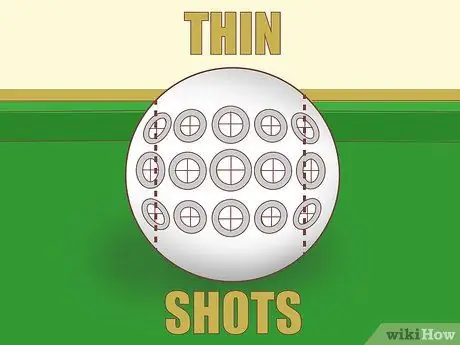
ขั้นตอนที่ 4. ระวังเมื่อถ่ายภาพแบบบาง
หากคุณต้องการตีลูกให้เต็มน้อยกว่า เป็นการยากที่จะประเมินจำนวนลูกที่เข้าได้ ยิ่งไปกว่านั้น ผลกระทบของมุมตัดนั้นรุนแรงมากจนข้อผิดพลาดเล็กๆ น้อยๆ จะเปลี่ยนมุมที่ได้ไปอย่างมาก ช็อตสัมผัสนี้ต้องใช้การฝึกฝนอย่างมากและทำงานได้ดีเมื่อคุณทราบจุดที่คุณต้องการแล้ว ถ้าเป็นไปได้ ให้หาช็อตอื่นที่จะถ่าย
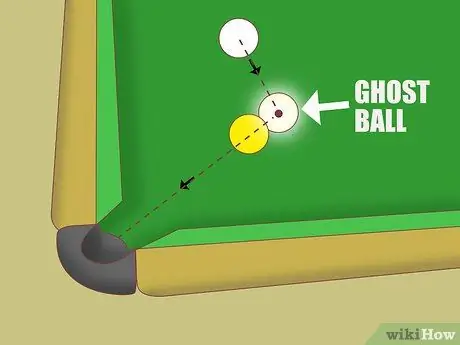
ขั้นตอนที่ 5. ลองใช้วิธีโกสต์บอลในการเล็ง
หากคำอธิบายความสมบูรณ์ของผลกระทบไม่สามารถช่วยคุณได้ ให้ลองใช้แนวทาง "ลูกผี":
- ลองนึกภาพว่ามีเส้นตรงจากกระเป๋าโต๊ะถึงกึ่งกลางของลูกบอลวัตถุ
- ขยายเส้นนี้ผ่านลูกบอลวัตถุเล็กน้อย ลองนึกภาพว่ามี "ลูกผี" ณ จุดนี้ อยู่บนเส้นและสัมผัสลูกบอลวัตถุ
- ในการเคาะลูกบอลวัตถุเข้าไปในกระเป๋า คุณต้องเล็งไปที่ศูนย์กลางของ "ลูกผี"
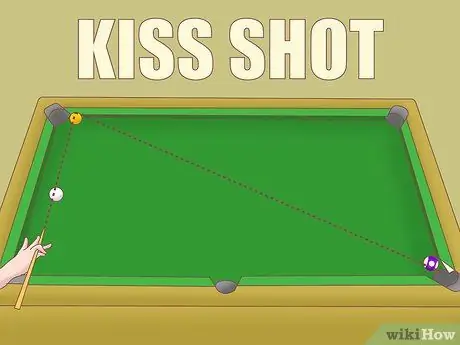
ขั้นตอนที่ 6. ใช้กฎข้อที่สามของช็อตช็อต
การจิกช็อตทำได้โดยการตีลูกบอลสีขาวกับลูกบอล A เพื่อให้เล็งและกระทบกับลูกบอล B หากคุณเล่นเกมที่อนุญาตให้จูบได้ ให้คำนึงถึงกฎนี้: ถ้าลูกบอล A กระทบราง มุมตัด ที่คุณตั้งเป้าไว้คือมุมที่ทำโดยลูกบอลสามลูก
ตัวอย่างเช่น หากมุมที่มีทรงกลม A เป็นจุดยอด 45º มุมตัดจะอยู่ที่ประมาณ 15º กฎความสมบูรณ์ข้างต้นระบุว่ามุมนี้สามารถสร้างได้ด้วยการชนกันเต็มที่
ส่วนที่ 3 จาก 3: การใช้ภาษาอังกฤษ (Side Twist)
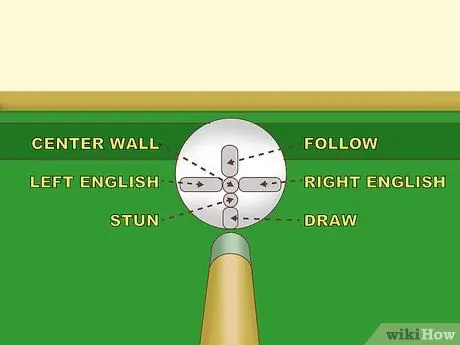
ขั้นตอนที่ 1. ทำให้ Poke ของคุณสมบูรณ์แบบก่อน
การกระตุ้นด้วยทัศนคติและเป้าหมายที่สม่ำเสมอควรมีความสำคัญสูงสุดหากคุณต้องการเล่นพูลอย่างจริงจัง ภาษาอังกฤษเป็นเทคนิคที่มีประโยชน์มาก แต่เอฟเฟกต์นั้นซับซ้อน และคุณต้องฝึกฝนอย่างสม่ำเสมอ
คุณจะมีช่วงเวลาที่ยากลำบากในการลดผลกระทบของภาษาอังกฤษให้แคบลงหากคุณไม่สามารถควบคุมแรงเหวี่ยงและการลื่นไถลได้ ผลกระทบนี้พิจารณาจากความสูงของจุดแทงของลูกบอล การลื่นไถลสามารถกำจัดได้อย่างสมบูรณ์โดยการกดจุดความยาวระหว่างจุดศูนย์กลางและส่วนบนของลูกบอล แต่เป็นเรื่องปกติที่ผู้เล่นจะตีที่จุดที่ระยะห่างนี้เพื่อการควบคุมและความเร็วที่เหมาะสมที่สุด
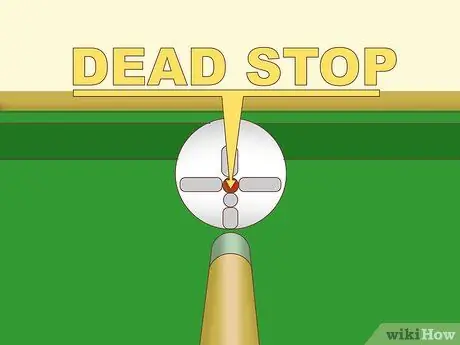
ขั้นตอนที่ 2. อยู่ห่างจากภาษาอังกฤษเมื่อลูกบอลสีขาวตกอยู่ในอันตรายจากการเข้าไปในกระเป๋า
หากไม่มีภาษาอังกฤษ ลูกบอลสีขาวจะหยุดโดยสมบูรณ์หลังจากการกระแทกโดยตรงอย่างสมบูรณ์ ฝึกการกระแทกโดยตรงโดยตีตรงกึ่งกลางของแกนแนวตั้งและแนวนอนของลูกบอลสีขาว เมื่อคุณได้ลูกบอลสีขาวเพื่อหยุดโดยสมบูรณ์ในแต่ละครั้ง คุณควรมีทักษะเพียงพอที่จะรวมภาษาอังกฤษไว้ในเกม
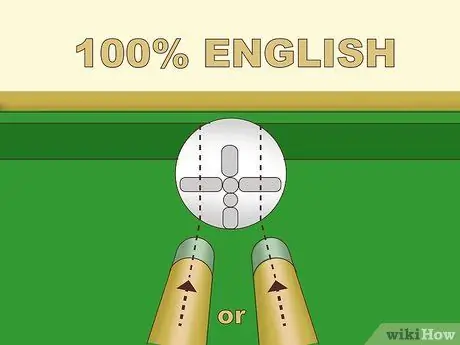
ขั้นตอนที่ 3 ฝึกฝนจุดแข็งภาษาอังกฤษต่างๆ
ภาษาอังกฤษมีหลายประเภท แต่บทความนี้กล่าวถึงเฉพาะรูปแบบพื้นฐานเท่านั้น ถ้าไม้จิ้มไปทางซ้ายของศูนย์กลางของลูกบอล ลูกบอลจะหมุนไปตามแกนนี้ นี่คือ "ภาษาอังกฤษที่เหลือ" เมื่อลูกหมุนนี้กระทบพื้นผิว การหมุนจะทำให้ลูกหมุนไปทางซ้ายมากกว่าไม่มีภาษาอังกฤษ ในทางกลับกัน การจิ้มไปทางขวาตรงกลางของลูกบอลสีขาวจะทำให้ "อิงลิชไรท์" และเด้งลูกบอลไปทางขวามากขึ้น ยิ่งคุณโผล่จากศูนย์กลางของลูกบอลมากเท่าไหร่ ผลกระทบก็จะยิ่งมากขึ้น:
- ภาษาอังกฤษ 100% หรือสูงสุด ทำได้โดยการจิ้มจุดกึ่งกลางระหว่างจุดศูนย์กลางและขอบของลูกบอล นี่คือระยะการสะกิดสูงสุดที่จะได้รับการกระตุ้นโดยมีข้อผิดพลาดน้อยที่สุด
- ภาษาอังกฤษ 50% ทำได้โดยจิ้มจุดกึ่งกลางระหว่างจุดสูงสุดกับศูนย์กลางของลูกบอล (¼ ระยะห่างระหว่างจุดศูนย์กลางถึงขอบของลูกบอล)
- คุณสามารถใช้เปอร์เซ็นต์ภาษาอังกฤษโดยจิ้มที่จุดต่างๆ ระหว่างจุดศูนย์กลางและจุดสูงสุดของลูกบอลสีขาว
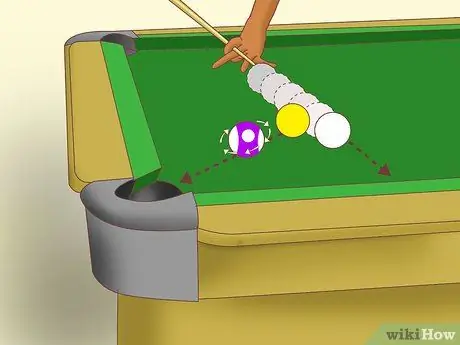
ขั้นตอนที่ 4 ทำความเข้าใจเกี่ยวกับการใส่เกียร์
เมื่อลูกบอลสองลูกชนกัน ลูกบอลวัตถุจะเริ่มหมุนบนแกนใดแกนหนึ่ง ตามมุมของจังหวะและปริมาณของภาษาอังกฤษที่ได้รับ หากคุณสามารถบรรลุ " การใส่เกียร์ " การหมุนนี้จะเกิดขึ้นตามแกนของการเคลื่อนที่ กล่าวอีกนัยหนึ่ง การเคลื่อนที่ของลูกวัตถุไม่ได้รับผลกระทบจากการหมุน ลูกบอลจะเลื่อนไปตาม "เส้นกึ่งกลาง" หรือเส้นที่ลากระหว่างจุดศูนย์กลางของลูกบอลทั้งสองเมื่อกระทบ
คำนี้มาจากการเปรียบเทียบระหว่างเกียร์สองเฟืองที่ทำงานประสานกันอย่างราบรื่นและส่งสัญญาณการเคลื่อนไหวได้อย่างสมบูรณ์แบบ
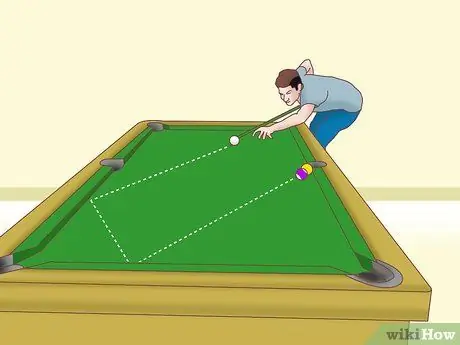
ขั้นตอนที่ 5. ปรับภาษาอังกฤษเพื่อให้เข้าเกียร์ได้ทุกชิ้น
เมื่อคุณได้ลูกเตะมุมโดยใช้วิธีการ "เต็ม" หรือ "ลูกผี" แล้ว ควรตรวจสอบให้แน่ใจว่าลูกบอลของวัตถุไม่หมุนอย่างผิดปกติและทำลายการยิงของคุณ นี่คือแผนภูมิที่สามารถช่วยคุณค้นหามุมที่เหมาะสมและภาษาอังกฤษได้ ตัวเลขด้านล่างทั้งหมดเป็น "ภาษาอังกฤษด้านนอก" ซึ่งหมายความว่าคุณขยับไม้ที่อยู่ถัดจากลูกบอลสีขาวให้ไกลกว่าลูกบอลวัตถุ
- หากมุมตัดเป็น15º ให้ใช้ภาษาอังกฤษมากกว่า 20% เล็กน้อย (จำไว้ว่ามุมตัดคือมุมระหว่างเส้นทางเริ่มต้นของลูกบอลสีขาวกับเส้นทางของลูกบอลของวัตถุ)
- หากมุมตัดเป็น 30º ให้ใช้ภาษาอังกฤษที่ 40%
- หากมุมตัดเป็น45º ให้ใช้ภาษาอังกฤษ 55%
- หากมุมตัดเป็น60º ให้ใช้ภาษาอังกฤษที่ 70%
- เมื่อมุมตัดเข้าใกล้ 90º ให้เพิ่มภาษาอังกฤษเป็น 80%
ขั้นตอนที่ 6 รู้ผลกระทบของการกระแทกโดยไม่ต้องใส่เกียร์
ถ้าคุณใช้ภาษาอังกฤษ น้อย ของ "เกียร์" จำนวนมากในขั้นตอนสุดท้าย ลูกบอลสีขาวจะเคลื่อนไปข้างหน้าในระหว่างการกระทบ และบิดด้านข้างเลื่อนไปที่ลูกบอลวัตถุ จากนั้น ลูกบอลของวัตถุจะเคลื่อนที่ไปทางขวาเล็กน้อยจากมุมตัดโดยประมาณ หากภาษาอังกฤษของคุณเป็นมากกว่าการใส่เกียร์ ลูกบอลของวัตถุจะเคลื่อนไปทางซ้ายเล็กน้อยของมุมตัดโดยประมาณ
- เอฟเฟกต์นี้เรียกว่าการโยนแบบเหนี่ยวนำโดยการตัด: มุมของการตัดจะแทนที่การบิดซึ่งทำให้ลูกบอลกลิ้งออกนอกเส้นทางเล็กน้อย
- คุณสามารถใช้เทคนิคนี้เพื่อสร้างภาพที่แทบจะเป็นไปไม่ได้ หากการยิงเพียงครั้งเดียวของคุณอยู่ทางขวามากเกินไป ให้เพิ่มภาษาอังกฤษของคุณเพื่อให้ลูกบอลเข้ากระเป๋า
เคล็ดลับ
- หากลูกบอลวัตถุติดอยู่กับรางและคุณต้องกลิ้งไปตามรางเข้าหากระเป๋า ให้ตีรางก่อนเสมอก่อนที่จะสัมผัสลูกบอลของวัตถุ ดังนั้น ลูกบอลสีขาวจึงให้โมเมนตัมแก่ราง มากกว่าไปทางมัน (หากมุมกระแทกเกิน 45º คุณจะต้องใช้ภาษาอังกฤษ)
- ยิ่งมุมของการกระแทกระหว่างสองลูกมากเท่าใด โมเมนตัมในการส่งก็จะยิ่งน้อยลงเท่านั้น ซึ่งหมายความว่าคุณจะต้องใช้แรงขึ้นเล็กน้อยสำหรับการตัดแบบบาง (รอยแตกที่มุมสุดขั้ว)
- หลังจากกระทบ มุมระหว่างเส้นทางของลูกบอลสีขาวกับเส้นทางของลูกบอลของวัตถุต้องเท่ากับ 90º เสมอ ใช้ความรู้นี้เพื่อป้องกันไม่ให้ลูกบอลสีขาวเข้าไปในถุง โปรดทราบว่าการบิดตัวที่รุนแรงสามารถทำลายกฎข้อนี้ และลูกบอลที่มีมวลต่างกัน (เช่น บนโต๊ะพูลทั่วไปในร้านกาแฟ)






