- ผู้เขียน Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:16.
- แก้ไขล่าสุด 2025-01-23 12:49.
ทุกคนสามารถเรียนคณิตศาสตร์ได้ไม่ว่าพวกเขาจะอยู่ในระดับสูงแล้วในโรงเรียนหรือผู้ที่ต้องการฝึกฝนพื้นฐานอีกครั้ง หลังจากพูดคุยถึงวิธีการเป็นผู้เรียนที่ดีในวิชาคณิตศาสตร์แล้ว บทความนี้จะสอนคุณเกี่ยวกับความก้าวหน้าทางคณิตศาสตร์ขั้นพื้นฐานและจะให้องค์ประกอบพื้นฐานที่คุณจำเป็นต้องเรียนรู้ในการฝึกฝนแต่ละครั้ง จากนั้น บทความนี้จะกล่าวถึงพื้นฐานการเรียนรู้เลขคณิต ซึ่งจะช่วยให้ทั้งเด็กประถมและทุกคนที่ต้องการเรียนรู้พื้นฐานของวิทยาศาสตร์สาขานี้
ขั้นตอน
ตอนที่ 1 ของ 6: กุญแจสู่การเป็นนักเรียนคณิตศาสตร์ที่ดี

ขั้นตอนที่ 1 ปรากฏในชั้นเรียน
เมื่อคุณขาดเรียน คุณควรเรียนรู้แนวคิดจากเพื่อนร่วมชั้นหรือจากหนังสือเรียนของคุณ คุณจะไม่ได้รับข้อความสรุปจากเพื่อนมากเท่ากับที่ได้รับจากครูของคุณ
- เข้าเรียนให้ตรงเวลา. ให้มาถึงแต่เช้าหน่อยแล้วเปิดสมุดบันทึกของคุณให้ถูกที่ เปิดหนังสือเรียนและหยิบเครื่องคิดเลขออกมา เพื่อให้คุณพร้อมที่จะเริ่มเมื่อครูของคุณพร้อมที่จะสอน
- เฉพาะในกรณีที่คุณป่วย ถ้าคุณขาดเรียนจริงๆ ให้ถามเพื่อนร่วมชั้นว่าครูกำลังพูดถึงอะไรและให้การบ้านอะไร

ขั้นตอนที่ 2 ทำงานกับครูของคุณ
หากครูของคุณกำลังแก้ไขปัญหาหน้าชั้นเรียน ให้ทำงานกับครูโดยแก้ไขปัญหาในสมุดบันทึกของคุณ
- ตรวจสอบให้แน่ใจว่าโน้ตของคุณชัดเจนและอ่านง่าย อย่าเพิ่งเขียนคำถาม จดสิ่งที่ครูพูดด้วยซึ่งสามารถปรับปรุงความเข้าใจของคุณเกี่ยวกับแนวคิดที่จะอธิบายได้
- กรอกตัวอย่างคำถามที่ได้รับจากครูของคุณ ขณะที่ครูเดินไปรอบๆ ชั้นเรียนในขณะที่คุณทำงาน ให้ตอบคำถามที่ถาม
- เข้าร่วมเมื่อครูแก้ปัญหา อย่ารอให้ครูโทรหาคุณ เสนอที่จะตอบเมื่อคุณรู้คำตอบ และยกมือขึ้นเพื่อถามคำถามหากคุณไม่แน่ใจเกี่ยวกับเนื้อหาที่สอน

ขั้นตอนที่ 3 ทำการบ้านของคุณในวันเดียวกับที่คุณได้รับการบ้าน
หากคุณทำการบ้านในวันเดียวกัน แนวคิดก็ยังสดใหม่อยู่ในใจของคุณ บางครั้งการบ้านของคุณให้เสร็จในวันเดียวกันนั้นเป็นไปไม่ได้ ทำการบ้านให้เสร็จก่อนไปเรียน

ขั้นตอนที่ 4 ทำงานนอกชั้นเรียนหากคุณต้องการความช่วยเหลือ
ไปเยี่ยมครูของคุณในช่วงพักหรือในเวลาราชการ
- หากคุณมีศูนย์คณิตศาสตร์ที่โรงเรียนของคุณ ให้ค้นหาเวลาเปิดทำการและขอความช่วยเหลือ
- เข้าร่วมกลุ่มการศึกษา กลุ่มการศึกษาที่ดีโดยทั่วไปประกอบด้วย 4 หรือ 5 คนที่มีความสามารถต่างกัน หากคุณเป็นนักเรียน "C" ในวิชาคณิตศาสตร์ เข้าร่วมกลุ่มนักเรียน 2 หรือ 3 คนที่ได้เกรด "A" หรือ "B" เพื่อจะได้พัฒนาทักษะของคุณ หลีกเลี่ยงการเข้าร่วมกลุ่มนักเรียนที่มีผลการเรียนต่ำกว่าคุณ
ตอนที่ 2 ของ 6: การเรียนคณิตศาสตร์ในโรงเรียน

ขั้นตอนที่ 1 เริ่มต้นด้วยเลขคณิต
ในโรงเรียนส่วนใหญ่ นักเรียนจะเรียนเลขคณิตในโรงเรียนประถม เลขคณิตครอบคลุมพื้นฐานของการบวก การลบ การคูณและการหาร
- ทำแบบฝึกหัดคำถาม การทำโจทย์เลขซ้ำแล้วซ้ำอีกเป็นวิธีที่ดีที่สุดในการจำพื้นฐานได้อย่างถูกต้อง มองหาซอฟต์แวร์ที่สามารถให้ปัญหาทางคณิตศาสตร์ที่หลากหลายแก่คุณได้ นอกจากนี้ ให้มองหาปัญหาเกี่ยวกับกรอบเวลาเพื่อปรับปรุงความเร็วของคุณ
- คุณยังสามารถค้นหาปัญหาทางคณิตศาสตร์ทางออนไลน์ และคุณสามารถดาวน์โหลดแอปเลขคณิตไปยังอุปกรณ์มือถือของคุณได้

ขั้นตอนที่ 2 ดำเนินการต่อด้วยพรีพีชคณิต
แบบฝึกหัดนี้จะช่วยให้คุณมีองค์ประกอบพื้นฐานที่จำเป็นสำหรับการแก้ปัญหาพีชคณิตในภายหลัง
- เรียนรู้เรื่องเศษส่วนและทศนิยม คุณจะได้เรียนรู้การบวก ลบ คูณ และหารเศษส่วนและทศนิยม เกี่ยวกับเศษส่วน คุณจะได้เรียนรู้วิธีลบเศษส่วนและแปลตัวเลขที่รวมกัน เกี่ยวกับทศนิยม คุณจะเข้าใจค่าของสถานที่ และคุณจะสามารถใช้ทศนิยมในปัญหาเรื่องได้
- เรียนรู้เกี่ยวกับอัตราส่วน สัดส่วน และเปอร์เซ็นต์ แนวคิดเหล่านี้จะช่วยให้คุณเรียนรู้การเปรียบเทียบ
- แนะนำตัวเองให้รู้จักกับเรขาคณิตพื้นฐาน คุณจะได้เรียนรู้รูปทรงและแนวคิด 3 มิติ คุณจะได้เรียนรู้แนวคิดต่างๆ เช่น พื้นที่ เส้นรอบรูป ปริมาตร และพื้นที่ผิว ตลอดจนข้อมูลเกี่ยวกับเส้นและมุมขนานและตั้งฉาก
- ทำความเข้าใจสถิติพื้นฐานบางอย่าง ในพีชคณิตก่อนกำหนด บทนำสู่สถิติโดยทั่วไปประกอบด้วยภาพ เช่น กราฟ แผนภูมิกระจาย แผนภูมิแผนภาพแสตมป์ และฮิสโตแกรม
- เรียนรู้พื้นฐานของพีชคณิต ซึ่งรวมถึงแนวคิดต่างๆ เช่น การแก้สมการง่าย ๆ ที่มีตัวแปร เรียนรู้เกี่ยวกับคุณสมบัติ เช่น คุณสมบัติการกระจาย การวาดสมการอย่างง่าย และการแก้ความไม่เท่าเทียมกัน
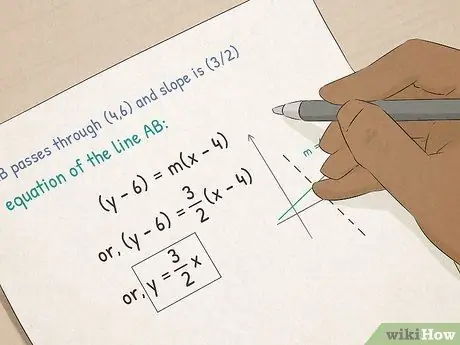
ขั้นตอนที่ 3 เลื่อนไปที่พีชคณิต I
ในปีแรกของพีชคณิต คุณจะได้เรียนรู้เกี่ยวกับสัญลักษณ์พื้นฐานที่รวมอยู่ในพีชคณิต คุณจะได้เรียนรู้ที่จะ:
- แก้สมการและอสมการที่มีตัวแปร คุณจะได้เรียนรู้วิธีแก้ปัญหาเหล่านี้บนกระดาษและวิธีแก้ปัญหาด้วยรูปภาพ
- แก้ปัญหาเรื่อง. คุณจะประหลาดใจกับปัญหาในชีวิตประจำวันที่คุณต้องเผชิญในอนาคตซึ่งต้องใช้ความสามารถในการแก้ปัญหาเรื่องพีชคณิต ตัวอย่างเช่น คุณจะใช้พีชคณิตเพื่อค้นหาอัตราดอกเบี้ยที่คุณได้รับจากบัญชีธนาคารหรือการลงทุนของคุณ คุณยังสามารถใช้พีชคณิตเพื่อหาว่าคุณควรเดินทางนานแค่ไหนโดยพิจารณาจากความเร็วของรถคุณ
- ทำงานกับเลขชี้กำลัง เมื่อคุณเริ่มแก้สมการพหุนาม (นิพจน์ที่มีตัวเลขและตัวแปร) คุณจะเข้าใจวิธีใช้เลขชี้กำลัง ซึ่งอาจรวมถึงแบบฝึกหัดที่มีสัญกรณ์วิทยาศาสตร์ด้วย เมื่อคุณเชี่ยวชาญเลขชี้กำลังแล้ว คุณสามารถเรียนรู้การบวก ลบ คูณ และหารนิพจน์พหุนามได้
- แก้ปัญหารากที่สองและรากที่สอง เมื่อคุณเชี่ยวชาญในหัวข้อนี้ คุณจะสามารถจดจำกำลังสองของตัวเลขจำนวนมากได้ คุณจะสามารถทำงานกับสมการที่มีรากที่สองได้
- เข้าใจฟังก์ชันและกราฟ ในพีชคณิต คุณจะได้เรียนรู้เกี่ยวกับสมการกราฟิก คุณจะได้เรียนรู้วิธีคำนวณความชันของเส้น การใส่สมการในรูปแบบจุด-ความชัน และวิธีการคำนวณการแบ่งส่วน x และ y ของเส้นโดยใช้แบบฟอร์มความชัน-ค่าตัดขวาง
- หาระบบสมการ บางครั้ง คุณจะได้รับสมการที่แตกต่างกัน 2 สมการพร้อมตัวแปร x และ y และคุณต้องแก้หา x หรือ y สำหรับสมการทั้งสอง โชคดีที่คุณจะได้เรียนรู้เทคนิคมากมายในการแก้สมการเหล่านี้ รวมถึงการสร้างกราฟ การแทนที่ และการบวก

ขั้นตอนที่ 4 ศึกษาเรขาคณิต
ในเรขาคณิต คุณจะได้เรียนรู้เกี่ยวกับคุณสมบัติของเส้น ส่วนโค้ง มุม และรูปร่าง
- คุณจะจำทฤษฎีบทและผลสืบเนื่องจำนวนหนึ่งที่จะช่วยให้คุณเข้าใจกฎของเรขาคณิต
- คุณจะได้เรียนรู้วิธีคำนวณพื้นที่ของวงกลม วิธีใช้ทฤษฎีบทพีทาโกรัส และวิธีค้นหาความสัมพันธ์ระหว่างมุมและด้านข้างของสามเหลี่ยมพิเศษ
- คุณจะเห็นคำถามเรขาคณิตมากมายในการทดสอบมาตรฐานในอนาคต เช่น SAT, ACT และ GRE
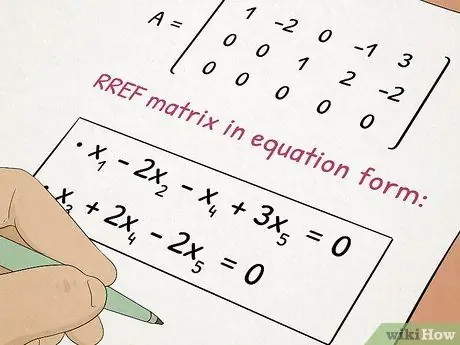
ขั้นตอนที่ 5. เรียนวิชาพีชคณิต II
พีชคณิต II สร้างขึ้นจากแนวคิดที่คุณได้เรียนรู้ในพีชคณิต I ในขณะที่เพิ่มหัวข้อที่ซับซ้อน เช่น สมการกำลังสองและเมทริกซ์
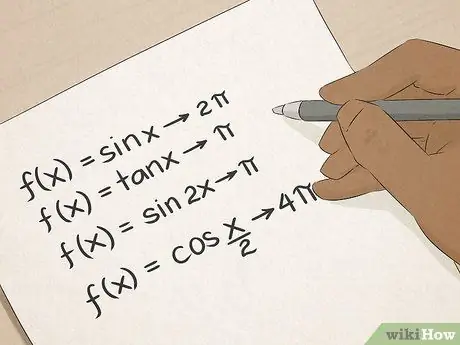
ขั้นตอนที่ 6 ตรีโกณมิติ
คุณรู้ศัพท์ตรีโกณมิติ: ไซน์ โคไซน์ แทนเจนต์ และอื่นๆ ตรีโกณมิติจะสอนวิธีการคำนวณมุมและความยาวเส้นที่ใช้งานได้จริงมากมาย และทักษะเหล่านี้จะประเมินค่าไม่ได้สำหรับผู้ที่ทำงานด้านการก่อสร้าง สถาปัตยกรรม วิศวกรรม หรือการสำรวจ
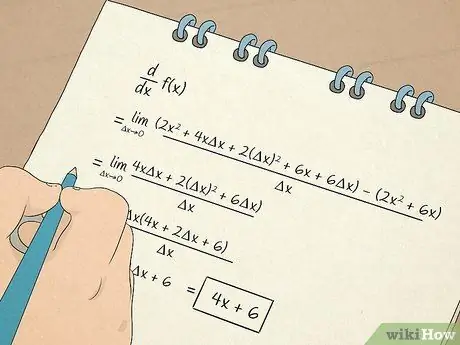
ขั้นตอนที่ 7 ทำการคำนวณแคลคูลัส
แคลคูลัสอาจฟังดูน่ากลัว แต่เป็นเครื่องมือที่ยอดเยี่ยมในการทำความเข้าใจพฤติกรรมของตัวเลขหรือโลกรอบตัวคุณ
- แคลคูลัสจะสอนฟังก์ชันและขีดจำกัดให้คุณ คุณจะเห็นจำนวนพฤติกรรมของฟังก์ชันที่มีประโยชน์ รวมทั้ง e^x และฟังก์ชันลอการิทึม
- คุณจะได้เรียนรู้วิธีการคำนวณและทำงานกับอนุพันธ์ อนุพันธ์อันดับแรกให้ข้อมูลตามความชันของเส้นสัมผัสไปยังสมการ ตัวอย่างเช่น อนุพันธ์จะบอกคุณถึงอัตราที่บางสิ่งเปลี่ยนแปลงในสถานการณ์ที่ไม่เป็นเชิงเส้น อนุพันธ์อันดับสองจะบอกคุณว่าฟังก์ชันเพิ่มขึ้นหรือลดลงในช่วงเวลาหนึ่ง เพื่อให้คุณสามารถกำหนดความเว้าของฟังก์ชันได้
- ปริพันธ์จะสอนวิธีคำนวณพื้นที่ใต้เส้นโค้งและปริมาตร
- แคลคูลัสในโรงเรียนมัธยมปลายโดยทั่วไปจะลงท้ายด้วยลําดับและลําดับ แม้ว่านักเรียนจะไม่เห็นแอปพลิเคชันมากมายสำหรับวงจร แต่วงจรก็มีความสำคัญสำหรับผู้ที่ศึกษาสมการเชิงอนุพันธ์
ส่วนที่ 3 จาก 6: ความรู้พื้นฐานทางคณิตศาสตร์--การบวกหลัก

ขั้นตอนที่ 1 เริ่มต้นด้วยข้อเท็จจริง "+1"
การบวก 1 เข้ากับตัวเลขจะนำคุณไปสู่จำนวนสูงสุดบนเส้นจำนวน ตัวอย่างเช่น 2+1 = 3
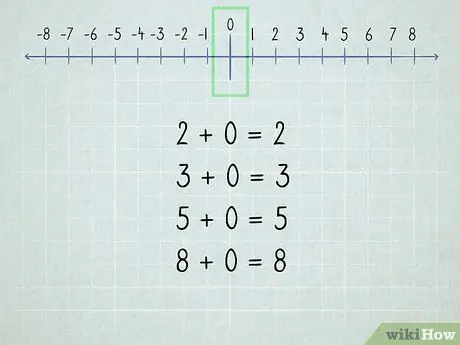
ขั้นตอนที่ 2 ทำความเข้าใจกับศูนย์
ตัวเลขทั้งหมดที่เติมลงในศูนย์เป็นตัวเลขเดียวกันเพราะ "ศูนย์" หมายถึง "ไม่มี"

ขั้นตอนที่ 3 เรียนรู้ตัวเลขคู่
ตัวเลขหลายตัวเป็นปัญหาที่เกี่ยวข้องกับการเพิ่มตัวเลขสองตัวที่เท่ากัน ตัวอย่างเช่น 3 + 3 = 6 เป็นตัวอย่างของสมการที่เกี่ยวข้องกับตัวเลขหลายตัว

ขั้นตอนที่ 4 ใช้การทำแผนที่เพื่อเรียนรู้เกี่ยวกับโซลูชันเพิ่มเติมอื่นๆ
ในตัวอย่างด้านล่าง คุณเรียนรู้โดยการทำแผนที่ว่าเกิดอะไรขึ้นเมื่อคุณบวก 3 กับ 5, 2 และ 1 ลองใช้ปัญหา "เพิ่มโดย 2" ด้วยตัวคุณเอง

ขั้นตอนที่ 5. ทำต่อไปจนเกิน 10
เรียนรู้การบวกตัวเลข 3 ตัวเข้าด้วยกันเพื่อให้ได้ตัวเลขที่มากกว่า 10
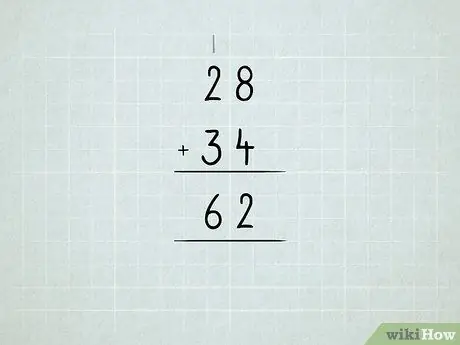
ขั้นตอนที่ 6 เพิ่มจำนวนที่มากขึ้น
เรียนรู้เกี่ยวกับการจัดกลุ่มใหม่เป็นสิบ หลักสิบเป็นร้อย และอื่นๆ
- บวกตัวเลขในคอลัมน์ด้านขวาก่อน 8 + 4 = 12 ซึ่งหมายความว่าคุณมี 1 หมายเลข 10 และ 2 หมายเลข 1 เขียนหมายเลข 2 ใต้คอลัมน์หน่วย
-
เขียนเลข 1 ในหลักสิบ
-
เพิ่มหลักสิบให้ครบถ้วน
ส่วนที่ 4 จาก 6: พื้นฐานทางคณิตศาสตร์--กลยุทธ์การลด

ขั้นตอนที่ 1. เริ่มต้นด้วย "ถอยหลัง 1 หลัก
การลบ 1 ออกจากตัวเลขจะนำคุณกลับ 1 ตัวเลข ตัวอย่างเช่น 4 - 1 = 3

ขั้นตอนที่ 2 เรียนรู้การลบเลขคู่
ตัวอย่างเช่น คุณบวกตัวเลข 5 + 5 เพื่อให้ได้ 10 แค่เขียนสมการไปข้างหลังก็ได้ 10 - 5 = 5
- ถ้า 5 + 5 = 10 แล้ว 10 - 5 = 5
-
ถ้า 2 + 2 = 4 แล้ว 4 - 2 = 2

ขั้นตอนที่ 3 จดจำข้อเท็จจริงเกี่ยวกับครอบครัว
ตัวอย่างเช่น:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

ขั้นตอนที่ 4. ค้นหาตัวเลขที่หายไป
ตัวอย่างเช่น _ + 1 = 6 (คำตอบคือ 5)

ขั้นตอนที่ 5. จดจำความเป็นจริงของการลบถึง 20

ขั้นตอนที่ 6 ฝึกลบตัวเลข 1 หลักจากตัวเลข 2 หลักโดยไม่ต้องยืม
ลบตัวเลขในคอลัมน์หลักและลดตัวเลขในคอลัมน์หลักสิบ
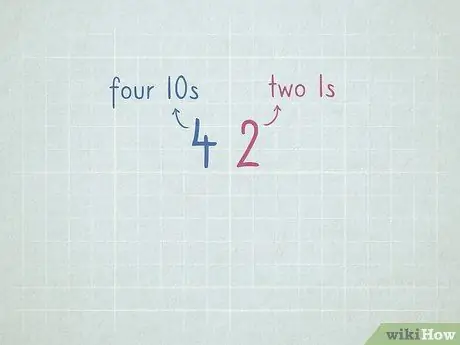
ขั้นที่ 7. ฝึกวางมูลค่าเตรียมลบด้วยการยืม
- 32 = 3 ตัวเลข 10 และ 2 ตัวเลข 1
- 64 = 6 ตัวเลข 10 และ 4 ตัวเลข 1
- 96 = _ หมายเลข 10 และ _ หมายเลข 1
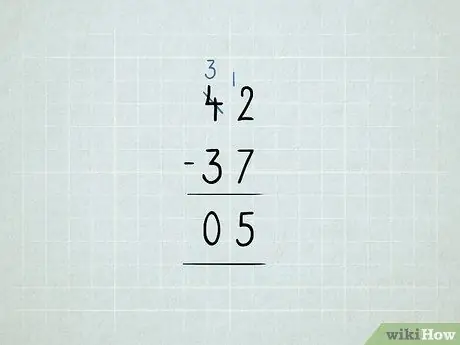
ขั้นตอนที่ 8 ลบด้วยการยืม
- คุณต้องการลบ 42 - 37 คุณเริ่มด้วยการพยายามลบ 2 - 7 ในคอลัมน์หน่วย ปรากฎว่าใช้งานไม่ได้!
-
ยืมเลข 10 จากหลักสิบ แล้วใส่ลงในหลักสิบ ตอนนี้คุณมี 3 10 แทนที่จะเป็น 4 10 ตอนนี้คุณมี 12 1 แทนที่จะเป็น 2 1
-
ลบคอลัมน์หน่วยของคุณก่อน: 12 - 7 = 5 จากนั้นตรวจสอบคอลัมน์หลักสิบ เนื่องจาก 3 - 3 = 0 คุณไม่จำเป็นต้องเขียนตัวเลข 0 คำตอบของคุณคือ 5
ตอนที่ 5 ของ 6: ความรู้พื้นฐานทางคณิตศาสตร์--การคูณปรมาจารย์

ขั้นตอนที่ 1 เริ่มต้นด้วยหมายเลข 1 และหมายเลข 0
ตัวเลขทั้งหมดที่คูณด้วย 1 จะเหมือนกับตัวเลขทั้งหมด จำนวนใดๆ ที่คูณด้วย 0 เท่ากับศูนย์

ขั้นตอนที่ 2 จดจำตารางสูตรคูณ

ขั้นตอนที่ 3 ฝึกโจทย์การคูณเลขตัวเดียว

ขั้นตอนที่ 4 คูณตัวเลข 2 หลักด้วยตัวเลข 1 หลัก
- คูณเลขล่างขวาด้วยเลขบนขวา
-
คูณเลขล่างขวาด้วยเลขบนซ้าย
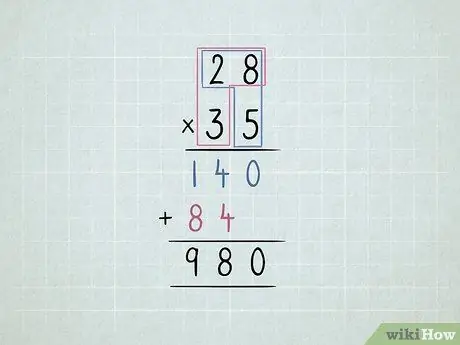
ขั้นตอนที่ 5. คูณตัวเลข 2 หลัก 2 ตัว
- คูณเลขล่างขวาด้วยเลขบนขวา แล้วตามด้วยเลขบนซ้าย
-
ย้ายแถวที่สองไปทางซ้ายหนึ่งหลัก
- คูณเลขล่างซ้ายด้วยเลขบนขวา แล้วตามด้วยเลขบนซ้าย
-
เพิ่มคอลัมน์ทั้งหมด
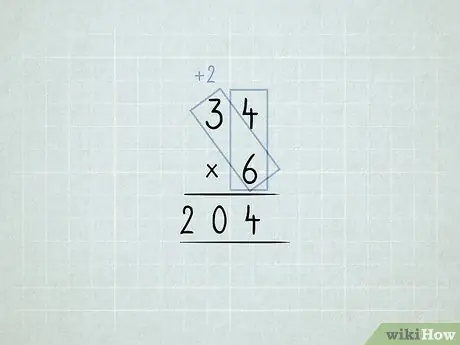
ขั้นตอนที่ 6 คูณและจัดกลุ่มคอลัมน์ใหม่
- คุณต้องการคูณ 34 x 6 คุณเริ่มต้นด้วยการคูณคอลัมน์หน่วย (4 x 6) แต่คุณไม่สามารถมี 24 1s ในคอลัมน์หน่วย
-
เก็บ 4 1s ในคอลัมน์หน่วย ย้าย 2 10s ไปยังหลักสิบ
-
คูณ 6 x 3 ซึ่งเท่ากับ 18 บวก 2 ที่คุณย้าย ซึ่งเท่ากับ 20
ส่วนที่ 6 จาก 6: ความรู้พื้นฐานทางคณิตศาสตร์ -- เปิดเผยปัญหาการหาร

ขั้นตอนที่ 1 คิดเกี่ยวกับการหารแทนที่จะคูณ
#* ถ้า 4 x 4 = 16 แล้ว 16 / 4 = 4
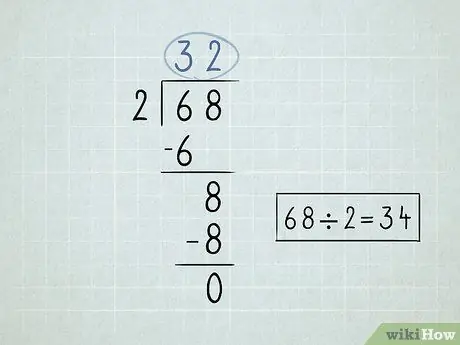
ขั้นตอนที่ 2 เขียนปัญหาการหารของคุณ
- หารตัวเลขทางด้านซ้ายของสัญลักษณ์การหารหรือตัวหารด้วยตัวเลขตัวแรกใต้สัญลักษณ์ตัวหาร เนื่องจาก 6 / 2 = 3 คุณจะต้องเขียนเลข 3 เหนือสัญลักษณ์หาร
-
คูณตัวเลขที่อยู่เหนือสัญลักษณ์หารด้วยตัวหาร นำผลลัพธ์ไปที่ด้านล่างของตัวเลขแรกภายใต้สัญลักษณ์หาร เนื่องจาก 3 x 2 = 6 คุณจะลดเลข 6 ลง
- ลบตัวเลข 2 ตัวที่คุณจดไว้ 6 - 6 = 0 คุณสามารถเว้น 0 ว่างไว้ได้ เนื่องจากโดยทั่วไปคุณจะไม่เริ่มตัวเลขด้วย 0
-
ดึงตัวเลขที่สองที่อยู่ใต้สัญลักษณ์หารลงมา
- หารจำนวนที่คุณนำมาลงด้วยตัวหาร ในกรณีนี้ 8 / 2 = 4 เขียนตัวเลข 4 เหนือสัญลักษณ์หาร
-
คูณตัวเลขบนขวาด้วยตัวหารแล้วดึงตัวเลขลงมา 4 x 2 = 8
-
ลบตัวเลขเหล่านั้น การลบขั้นสุดท้ายจะคืนค่าศูนย์ ซึ่งหมายความว่าคุณได้แก้ไขปัญหาแล้ว 68 x 2 = 34.

ขั้นตอนที่ 3 คำนวณส่วนที่เหลือด้วย
ตัวหารบางตัวไม่ได้แบ่งออกเป็นตัวเลขอื่นทั้งหมด หากคุณทำการลบครั้งสุดท้ายแล้ว และคุณไม่มีตัวเลขที่จะได้มาอีกต่อไป ตัวเลขสุดท้ายคือจำนวนที่เหลือ






