- ผู้เขียน Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:25.
- แก้ไขล่าสุด 2025-06-01 06:08.
การหารด้วยเลขฐานสิบดูยากในตอนแรกเพราะไม่มีใครสอน “0, 7 ตารางคูณ” ให้คุณ เคล็ดลับในการทำเช่นนี้คือการแปลงปัญหาการหารให้อยู่ในรูปแบบที่ใช้เฉพาะตัวเลขทั้งหมดเท่านั้น หลังจากที่คุณเขียนปัญหาใหม่ด้วยวิธีนี้ มันจะกลายเป็นปัญหาการหารยาวปกติ
ขั้นตอน
ส่วนที่ 1 ของ 2: การเขียนปัญหาเป็นปัญหากองสามัญ
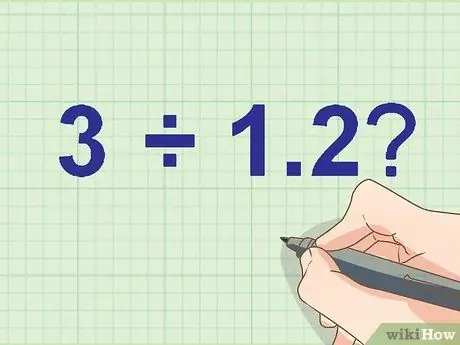
ขั้นตอนที่ 1 เขียนปัญหาการหารของคุณ
ใช้ดินสอถ้าคุณต้องการปรับปรุงงานของคุณ
-
ตัวอย่าง:
เท่าไหร่ 3 ÷ 1, 2?

ขั้นตอนที่ 2 เขียนจำนวนเต็มเป็นทศนิยม
เขียนจุดทศนิยมหลังจำนวนเต็ม แล้วเขียนศูนย์หลังจุดทศนิยม ทำเช่นนี้จนกว่าตัวเลขทั้งสองจะมีค่าตำแหน่งเดียวกันทางด้านขวาของจุดทศนิยม ซึ่งจะไม่เปลี่ยนค่าจำนวนเต็ม
-
ตัวอย่าง:
ในโจทย์ที่ 3 1, 2 จำนวนเต็มของเราคือ 3 เนื่องจาก 1, 2 มีค่าหลักทางขวาของจุดทศนิยม เขียน 3 เป็น 3, 0 เพื่อให้ตัวเลขนี้มีค่าหลักหนึ่งหลังทศนิยมด้วย ตอนนี้เรื่องของเรากลายเป็น 3, 0 ÷ 1, 2.
- คำเตือน: อย่าเพิ่มศูนย์ทางด้านซ้ายของจุดทศนิยม! ตัวเลข 3 เท่ากับ 3, 0 หรือ 3, 00 แต่ไม่เท่ากับ 30 หรือ 300

ขั้นตอนที่ 3 เลื่อนจุดทศนิยมไปทางขวาจนกว่าคุณจะได้จำนวนเต็ม
ในปัญหาการหาร คุณสามารถย้ายจุดทศนิยมได้ แต่เฉพาะในกรณีที่คุณย้ายจุดทศนิยมของตัวเลขทั้งหมดด้วยจำนวนขั้นที่เท่ากัน วิธีนี้ช่วยให้คุณแปลงปัญหาเป็นจำนวนเต็มได้
-
ตัวอย่าง:
ในการแปลง 3, 0 1, 2 เป็นจำนวนเต็ม ให้เลื่อนจุดทศนิยมไปทางขวาหนึ่งขั้น ดังนั้น 3, 0 กลายเป็น 30 และ 1, 2 กลายเป็น 12 ทีนี้ ปัญหาของเรากลายเป็น 30 ÷ 12.

ขั้นตอนที่ 4 เขียนปัญหาโดยใช้การหารยาว
วางตัวเลขที่หารได้ (โดยปกติจะเป็นตัวเลขที่มากกว่า) ใต้สัญลักษณ์การหารยาว เขียนเลขตัวหารนอกสัญลักษณ์นี้ ตอนนี้ คุณมีปัญหาการหารยาวแบบปกติที่ใช้จำนวนเต็ม หากคุณต้องการการช่วยเตือนเกี่ยวกับวิธีการหารยาว โปรดอ่านหัวข้อถัดไป
ส่วนที่ 2 ของ 2: การแก้ปัญหาการหารยาว

ขั้นตอนที่ 1 ค้นหาตัวเลขตัวแรกของคำตอบ
เริ่มแก้ปัญหานี้ตามปกติโดยเปรียบเทียบตัวหารกับหลักแรกของตัวเลขที่หาร คำนวณผลลัพธ์ของการหารหลักแรกนี้ด้วยจำนวนของตัวหาร แล้วเขียนผลลัพธ์เหนือหลักนั้น
ตัวอย่าง: เรากำลังพยายามหาร 30 ด้วย 12 เปรียบเทียบ 12 กับหลักแรกของตัวเลขหาร ซึ่งก็คือ 3 เนื่องจาก 12 มากกว่า 3, 3 หารด้วย 12 เท่ากับ 0 เขียนลงไป 0 ด้านบน 3 ในบรรทัดคำตอบ
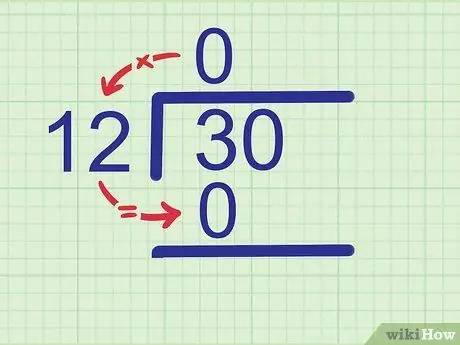
ขั้นตอนที่ 2 คูณผลหารด้วยตัวหาร
เขียนผลคูณของผลิตภัณฑ์ภายใต้จำนวนที่หาร เขียนผลลัพธ์ใต้หลักแรกของตัวเลขที่คุณหาร เนื่องจากเป็นตัวเลขที่คุณเพิ่งเห็น
-
ตัวอย่าง:
ตั้งแต่ 0 x 12 = 0 เขียน 0 ต่ำกว่า 3
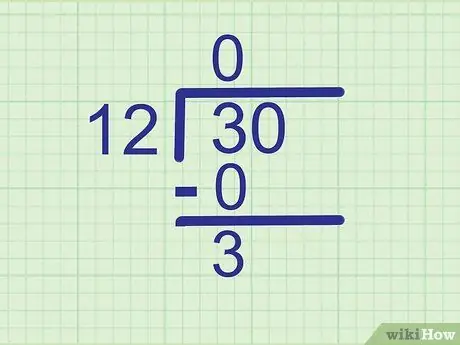
ขั้นตอนที่ 3 ลบเพื่อหาส่วนที่เหลือ
ลบผลิตภัณฑ์ที่คุณเพิ่งคำนวณจากตัวเลขด้านบนโดยตรง เขียนคำตอบในบรรทัดใหม่ด้านล่าง
-
ตัวอย่าง:
3 - 0 = 3 เขียนว่า
ขั้นตอนที่ 3 ต่ำกว่า 0
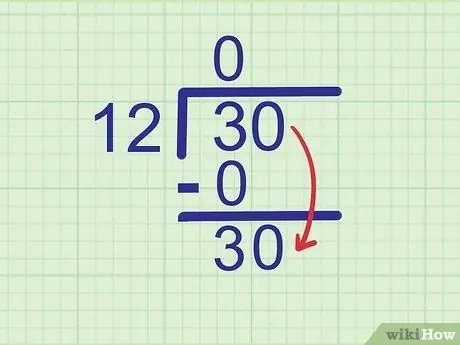
ขั้นตอนที่ 4 ลดตัวเลขถัดไป
วางหลักถัดไปของตัวเลขที่แบ่งถัดจากตัวเลขที่คุณเพิ่งจดไว้
-
ตัวอย่าง:
จำนวนที่หารคือ 30 เราเคยเห็นเลข 3 แล้ว หลักต่อไปที่ต้องลดคือ 0 ลดเลข 0 ไปข้าง 3 ให้กลายเป็น
ขั้นตอนที่ 30.
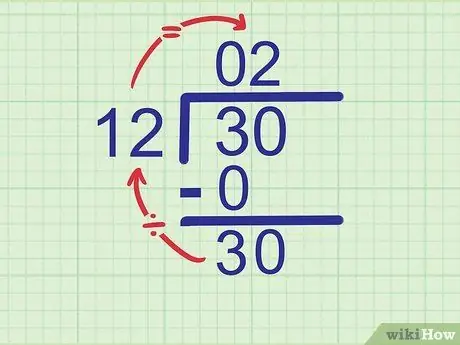
ขั้นตอนที่ 5. ลองหารตัวเลขใหม่ด้วยตัวหาร
ทวนซ้ำขั้นตอนแรกในส่วนนี้เพื่อค้นหาตัวเลขหลักที่สองของคำตอบของคุณ คราวนี้ เปรียบเทียบตัวหารกับตัวเลขที่คุณเพิ่งเขียนลงในแถวล่าง
-
ตัวอย่าง:
ผลหารของ 30 คูณ 12 คืออะไร? คำตอบที่ใกล้เคียงที่สุดที่เราหาได้คือ 2 เพราะ 12 x 2 = 24 เขียน
ขั้นตอนที่ 2. อันดับที่สองในบรรทัดคำตอบ
- หากคุณไม่แน่ใจในคำตอบ ให้ลองคูณหลายๆ ครั้งจนกว่าคุณจะพบคำตอบที่ตรงที่สุด ตัวอย่างเช่น หากค่าประมาณของคุณคือ 3 ให้คำนวณ 12 x 3 แล้วคุณได้ 36 ตัวเลขนี้มากเกินไปเพราะเรากำลังพยายามคำนวณ 30 ลองลดจำนวนหนึ่งลง 12 x 2 = 24 ตัวเลขนี้พอดี ดังนั้น 2 เป็นคำตอบที่ถูกต้อง

ขั้นตอนที่ 6 ทำซ้ำขั้นตอนข้างต้นเพื่อค้นหาหมายเลขถัดไป
นี่เป็นกระบวนการแบ่งยาวแบบเดียวกับที่ใช้ข้างต้น และสำหรับปัญหาการหารยาวใดๆ:
- คูณตัวเลขใหม่ของคำตอบของคุณด้วยตัวหาร: 2 x 12 = 24
- เขียนผลิตภัณฑ์ในบรรทัดใหม่ ใต้ตัวเลขที่หาร: เขียน 24 ต่ำกว่า 30
- ลบแถวล่างสุดจากแถวด้านบน: 30 - 24 = 6 ดังนั้น เขียน 6 ในแถวใหม่ด้านล่าง

ขั้นตอนที่ 7 ทำขั้นตอนนี้ต่อไปจนกว่าคุณจะกรอกคำตอบบรรทัดสุดท้าย
หากยังมีตัวเลขเหลืออยู่ในจำนวนที่แบ่ง ให้ลดตัวเลขลงและดำเนินการแก้ไขปัญหาต่อไปในลักษณะเดียวกัน หากคุณได้คำตอบในบรรทัดสุดท้ายแล้ว ให้ทำตามขั้นตอนต่อไป
-
ตัวอย่าง:
เราเพิ่งเขียน
ขั้นตอนที่ 2. ในบรรทัดคำตอบสุดท้าย ดำเนินการในขั้นตอนต่อไป

ขั้นตอนที่ 8 เพิ่มทศนิยมเพื่อ "ขยาย" จำนวนที่หารถ้าจำเป็น
หากจำนวนนั้นหารลงตัว ผลลัพธ์การลบขั้นสุดท้ายของคุณคือ “0” นั่นหมายความว่า คุณหารเสร็จแล้วและได้คำตอบในรูปของจำนวนเต็ม อย่างไรก็ตาม หากคุณกรอกคำตอบในบรรทัดสุดท้ายแล้วและยังมีตัวเลขที่แบ่งได้ คุณจะต้อง "ขยาย" ตัวเลขที่หารด้วยการเพิ่มจุดทศนิยมตามด้วยตัวเลข 0 โปรดจำไว้ว่าสิ่งนี้ไม่ ไม่ได้เปลี่ยนค่าของตัวเลข
-
ตัวอย่าง:
เรามาถึงบรรทัดสุดท้ายของคำตอบแล้ว แต่คำตอบสำหรับการลบครั้งสุดท้ายคือ "6" เขียน “6, 0” ใต้สัญลักษณ์การหารยาวโดยเติม “, 0” ที่หลักสุดท้าย เขียนจุดทศนิยมในตำแหน่งเดียวกันบนบรรทัดคำตอบ แต่อย่าเขียนอะไรหลังจากนั้น

ขั้นตอนที่ 9 ทำซ้ำขั้นตอนเดิมเพื่อค้นหาตัวเลขถัดไป
ข้อแตกต่างเพียงอย่างเดียวที่นี่คือ คุณต้องเพิ่มจุดทศนิยมในตำแหน่งเดียวกันบนบรรทัดคำตอบ เมื่อคุณทำเสร็จแล้ว คุณสามารถค้นหาตัวเลขคำตอบที่เหลือได้ด้วยวิธีเดียวกัน
-
ตัวอย่าง:
วาง 0 ใหม่ลงไปที่บรรทัดสุดท้ายเพื่อให้กลายเป็น "60" เนื่องจาก 60 หารด้วย 12 เท่ากับ 5 เขียน
ขั้นตอนที่ 5 เป็นตัวเลขสุดท้ายของบรรทัดคำตอบของเรา อย่าลืมว่าเราใส่ทศนิยมในบรรทัดคำตอบของเรา ดังนั้น, 2, 5 คือคำตอบสุดท้ายสำหรับคำถามของเรา
เคล็ดลับ
- คุณสามารถเขียนสิ่งนี้เป็นส่วนที่เหลือได้ (ดังนั้นคำตอบของ 3 1, 2 คือ “2 เหลือ 6”) อย่างไรก็ตาม เนื่องจากคุณกำลังใช้ทศนิยม ครูของคุณอาจคาดหวังให้คุณใช้ส่วนทศนิยมของคำตอบ
- หากคุณทำตามวิธีการหารยาวอย่างถูกต้อง คุณจะมีจุดทศนิยมอยู่ในตำแหน่งที่ถูกต้อง หรือจะไม่มีจุดทศนิยมเลยหากจำนวนนั้นหารด้วยหารลงตัวลงตัว อย่าพยายามเดาตำแหน่งทศนิยม ตำแหน่งทศนิยมมักจะแตกต่างจากตำแหน่งทศนิยมในจำนวนเริ่มต้นของคุณ
- ถ้าปัญหาการหารยาวไม่อยู่นาน คุณสามารถหยุดและปัดเศษเป็นตัวเลขที่ใกล้ที่สุด ตัวอย่างเช่น ในการแก้โจทย์ 17 4, 2 ให้นับเป็น 4.047… และปัดเศษคำตอบเป็น “ประมาณ 4.05”
-
จำเงื่อนไขการแบ่งของคุณ:
- จำนวนที่จะแบ่งคือจำนวนที่จะแบ่ง
- ตัวหารคือจำนวนที่ใช้หาร
- ผลหารคือคำตอบของปัญหาการหารคณิตศาสตร์
- ทั้งหมด: หารด้วยตัวหาร = ผลหาร
คำเตือน
จำไว้ว่า 30 12 จะให้คำตอบเดียวกับ 3 1, 2 อย่าพยายาม "แก้ไข" คำตอบของคุณหลังจากเลื่อนทศนิยมไปข้างหลัง
บทความวิกิฮาวที่เกี่ยวข้อง
- การแปลงเศษส่วนร่วมเป็นทศนิยม
- การทำดิวิชั่นระยะยาว
- หารเศษส่วนด้วยเศษส่วน
- การหารเศษส่วนผสม






