3 วิธีในการคำนวณความเร็ว

2024 ผู้เขียน: Jason Gerald | [email protected]. แก้ไขล่าสุด: 2024-01-16 20:01

ความเร็วคือการคำนวณว่าบางสิ่งเคลื่อนที่เร็วแค่ไหนในคราวเดียว หากคุณเคยดูมาตรวัดความเร็วของรถที่กำลังเคลื่อนที่ คุณจะเห็นการนับความเร็ว ยิ่งเข็มเดินทางมากเท่าใด ความเร็วของรถก็จะยิ่งสูงขึ้น มีหลายวิธีในการคำนวณความเร็ว ขึ้นอยู่กับประเภทของข้อมูลที่คุณมี โดยทั่วไปแล้วสูตร ความเร็ว = ระยะทาง/เวลา (หรือ k = j/w) เป็นวิธีที่ง่ายที่สุดในการคำนวณความเร็ว

ขั้นตอน

วิธีที่ 1 จาก 3: การใช้สูตรคำนวณความเร็วมาตรฐาน

ขั้นตอนที่ 1 ค้นหาระยะทางที่วัตถุเดินทาง

สูตรพื้นฐานที่คนส่วนใหญ่ใช้เพื่อค้นหาความเร็วของบางสิ่งนั้นใช้งานง่ายมาก ก่อนอื่น คุณจำเป็นต้องรู้ว่า “วัตถุที่วัดได้เดินทางเป็นระยะทางเท่าใด” กล่าวอีกนัยหนึ่ง ระยะห่างระหว่างจุดเริ่มต้นกับจุดสิ้นสุดของวัตถุคือเท่าใด

สูตรนี้เข้าใจง่ายผ่านตัวอย่าง สมมติว่าเราเดินทางโดยรถยนต์ไปยังสนามเด็กเล่น "161 กิโลเมตร" ในไม่กี่ขั้นตอน เราสามารถใช้ข้อมูลนี้เพื่อคำนวณสูตรให้สมบูรณ์

ขั้นตอนที่ 2 หาเวลาที่วัตถุเดินทางเป็นระยะทางนั้น

ข้อมูลต่อไปที่คุณต้องการคือระยะเวลาที่วัตถุไปถึงระยะทางที่กำหนด กล่าวอีกนัยหนึ่ง ใช้เวลานานเท่าใดกว่าวัตถุจะเคลื่อนที่จากจุดเริ่มต้นไปยังจุดสิ้นสุด

ในตัวอย่างนี้ สมมติว่าวัตถุใช้เวลาประมาณ สองชั่วโมง เพื่อไปให้ถึงที่หมาย

ขั้นตอนที่ 3 หารระยะทางตามเวลาที่ใช้เพื่อหาความเร็วของวัตถุ

คุณต้องการข้อมูลสองชิ้นนี้เท่านั้นจึงจะทราบความเร็วของวัตถุ ระยะทางต่อเวลาเท่ากับความเร็วของวัตถุ

ในตัวอย่างนี้ 161 กิโลเมตร/2 ชั่วโมง = 80.5 กิโลเมตร/ชั่วโมง.

ขั้นตอนที่ 4 อย่าลืมหน่วยที่ใช้

การใช้หน่วยที่ถูกต้องในคำตอบเป็นสิ่งสำคัญมาก (เช่น กิโลเมตรต่อชั่วโมง เป็นต้น) หากไม่มีหน่วยเหล่านี้ ผู้คนจะเข้าใจความหมายของคำตอบของคุณได้ยากมาก นอกจากนี้คุณยังสามารถเสียคะแนนได้หากคุณใช้หน่วยที่ไม่ถูกต้องเมื่อทำงานที่ได้รับมอบหมายจากโรงเรียน

หน่วยของความเร็วคือ หน่วยของระยะทางต่อหน่วยของเวลา. ตัวอย่างเช่น เนื่องจากเราวัดระยะทางเป็นกิโลเมตร และเวลาเป็นชั่วโมง หน่วยที่ใช้คือ กิโลเมตร/ชั่วโมง (หรือ กิโลเมตรต่อชั่วโมง).

วิธีที่ 2 จาก 3: การแก้ปัญหาการคำนวณที่ยากขึ้น

ขั้นตอนที่ 1 ค้นหาตัวแปรต่างๆ เพื่อแก้ปัญหาระยะทางและเวลา

เมื่อคุณเข้าใจสูตรพื้นฐานสำหรับความเร็วแล้ว คุณสามารถใช้สูตรนี้ในการคำนวณอื่นๆ ที่ไม่ใช่ความเร็วได้ ตัวอย่างเช่น หากในตอนแรกคุณทราบเพียงความเร็วของวัตถุและตัวแปรอื่น คุณสามารถจัดเรียงสูตรด้านบนใหม่เพื่อค้นหาข้อมูลที่ไม่รู้จักได้

• ตัวอย่างเช่น สมมติว่าเรารู้ว่ารถไฟเดินทางด้วยความเร็ว 20 กิโลเมตรต่อชั่วโมงเป็นเวลาสี่ชั่วโมง แต่เราไม่รู้ว่ามันเดินทางได้ไกลแค่ไหน หากต้องการทราบ เราสามารถจัดเรียงสูตรใหม่ได้ด้วยวิธีต่อไปนี้:

  ความเร็ว = ระยะทาง/เวลา

  ความเร็ว × เวลา = (ระยะทาง/เวลา) × เวลา

  ความเร็ว × เวลา = ระยะทาง

  20 กม./ชม. × 4 ชั่วโมง = ระยะทาง = 80 กิโลเมตร

ขั้นตอนที่ 2 แปลงหน่วยที่คุณใช้ตามต้องการ

บางครั้ง คุณอาจคำนวณความเร็วโดยใช้หน่วยหนึ่ง แต่ต้องแปลงเป็นหน่วยอื่น ในกรณีนี้ คุณต้องใช้ตัวประกอบการแปลงเพื่อให้ได้คำตอบตามหน่วยที่ถูกต้อง เมื่อต้องการทำสิ่งนี้ ให้เขียนความสัมพันธ์ระหว่างหน่วยในรูปเศษส่วนแล้วคูณ เมื่อคูณ ให้กลับเศษส่วนตามต้องการเพื่อเอาหน่วยที่ไม่ต้องการออก วิธีนี้ง่ายกว่าเสียงมาก!

• ตัวอย่างเช่น สมมติว่าในปัญหาตัวอย่างด้านบน เราต้องการคำตอบเป็นหน่วยไมล์แทนที่จะเป็นกิโลเมตร หนึ่งไมล์เท่ากับ 1.6 กิโลเมตร ดังนั้น เราสามารถแปลงได้ดังนี้

  80 กิโลเมตร × 1 ไมล์/1.6 กิโลเมตร = 50 ไมล์

• โปรดจำไว้ว่า เนื่องจากกิโลเมตรปรากฏที่ด้านล่างของเศษส่วน มันจึงลบกิโลเมตรออกจากคำตอบก่อนหน้า ดังนั้นผลลัพธ์สุดท้ายจึงใช้ไมล์
• เว็บไซต์นี้มีคุณลักษณะการแปลงสำหรับหน่วยที่ใช้กันทั่วไปส่วนใหญ่

ขั้นตอนที่ 3 แทนที่ตัวแปร "ระยะทาง" ด้วยสูตรระยะทางตามต้องการ

วัตถุไม่ได้เคลื่อนที่เป็นเส้นตรงและเรียบเสมอไป หากเป็นจริง คุณอาจไม่สามารถป้อนค่าตัวเลขเป็นหน่วยของระยะทางลงในสูตรความเร็วมาตรฐานได้ง่ายๆ อย่างไรก็ตาม คุณอาจต้องแทนที่ตัวอักษร j ในสูตร k = j/w ด้วยสูตรที่คล้ายกับระยะทางที่วัตถุเคลื่อนที่

• ตัวอย่างเช่น สมมติว่าเครื่องบินหมุนในอากาศเป็นระยะทาง 20 ไมล์ 5 ครั้ง เครื่องบินเสร็จสิ้นรอบในครึ่งชั่วโมง ในตัวอย่างนี้ เรายังต้องหาระยะทางทั้งหมดที่เครื่องบินเดินทางก่อนที่เราจะกำหนดความเร็วได้ เราสามารถใช้สูตรคำนวณระยะทางรอบวงกลม (ระยะทางรอบวงกลม) แทน j ในสูตรนี้ได้ สูตรนี้คือ เส้นรอบวง = 2πr โดยที่ r = รัศมีของวงกลม นี่คือวิธีแก้ปัญหา:

  k = (2 × × r)/w

  k = (2 × × 10)/0.5

  k = 62.83/0.5 = 125.66 ไมล์/ชั่วโมง

ขั้นตอนที่ 4 เข้าใจว่า k = j/w ให้ความเร็วเฉลี่ย

สูตรที่ง่ายและเรียบง่ายที่เราใช้เพื่อค้นหาความเร็วมีข้อเสียอยู่หนึ่งข้อ ค่าที่ได้คือความเร็วเฉลี่ยในทางเทคนิค ซึ่งหมายความว่าสูตรจะถือว่าวัตถุที่คุณกำลังวัดนั้นใช้ความเร็วเดียวกันกับที่วัตถุเคลื่อนที่ ดังที่เราเห็นด้านล่าง การหาความเร็วของวัตถุในช่วงเวลาเดียวจะยากขึ้นมาก

เพื่อแสดงให้เห็นความแตกต่างนี้ ลองนึกภาพครั้งสุดท้ายที่คุณเดินทางโดยรถยนต์ ไม่น่าเป็นไปได้ที่คุณจะเดินทางด้วยความเร็วเท่าๆ กับที่กำลังเดินทาง อย่างไรก็ตาม โดยปกติแล้ว คุณจะเริ่มต้นการเดินทางด้วยความเร็วต่ำและค่อยๆ เพิ่มความเร็วระหว่างทาง หยุดเนื่องจากไฟแดง การจราจรติดขัด ฯลฯ หากคุณใช้สูตรความเร็วมาตรฐานเพื่อค้นหาความเร็วระหว่างการเดินทาง จะไม่สามารถตรวจจับการเปลี่ยนแปลงของความเร็วนั้นได้ อย่างไรก็ตาม คุณจะได้รับคำตอบที่แสดงความเร็วเฉลี่ยของความแตกต่างของความเร็วทั้งหมดที่คุณเดินทาง

วิธีที่ 3 จาก 3: การคำนวณความเร็วทันที

บันทึก:

ส่วนนี้ใช้เทคนิคที่ไม่คุ้นเคยสำหรับผู้ที่ไม่เคยเรียนแคลคูลัส อ่านบทความของเราเกี่ยวกับแคลคูลัสเพื่อขอความช่วยเหลือ

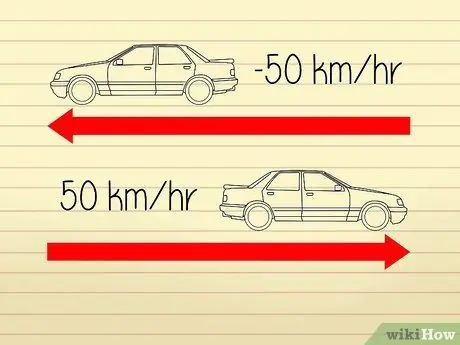
ขั้นตอนที่ 1 เข้าใจว่าความเร็วถูกกำหนดให้เป็นอัตราเร่ง

การคำนวณความเร็วสูงค่อนข้างสับสน เนื่องจากนักคณิตศาสตร์และนักวิทยาศาสตร์ใช้คำจำกัดความที่แตกต่างกันเพื่ออธิบาย "ความเร็ว" และ "ความเร่ง" การเร่งความเร็วมีสององค์ประกอบ: "อัตรา" และ "ทิศทาง" อัตราเท่ากับความเร็วของวัตถุ การเปลี่ยนทิศทางจะทำให้อัตราเร่งเปลี่ยนแปลง แต่ความเร็วจะไม่เปลี่ยนแปลง

• ตัวอย่างเช่น สมมุติว่ารถสองคันกำลังเคลื่อนที่ไปในทิศทางตรงกันข้าม มาตรวัดความเร็วของรถทั้งสองคันแสดงตัวเลข 50 กม./ชม. ดังนั้นทั้งคู่จึงเดินทางด้วยความเร็วเท่ากัน อย่างไรก็ตาม เนื่องจากรถยนต์กำลังเคลื่อนออกจากกัน เราสามารถพูดได้ว่ารถคันหนึ่งมี "อัตราเร่ง" ที่ -50 กม./ชม. ในขณะที่อีกคันมี "อัตราเร่ง" ที่ 50 กม./ชม.
• เช่นเดียวกับการคำนวณความเร็วในทันที คุณยังสามารถทำการคำนวณความเร่งในทันทีได้อีกด้วย

ขั้นตอนที่ 2 ใช้ค่าสัมบูรณ์เพื่อวัดความเร่งเชิงลบ

วัตถุสามารถมีอัตราการเร่งเป็นลบได้ (หากเคลื่อนที่ไปในทิศทางลบเมื่อเทียบกับวัตถุอื่น) อย่างไรก็ตาม ไม่มีความเร็วติดลบ ดังนั้น ในกรณีนี้ ค่าสัมบูรณ์ของอัตราจะระบุความเร็วของวัตถุ

ด้วยเหตุนี้ในปัญหาตัวอย่างข้างต้น รถทั้งสองคันจึงมีความเร็วเท่ากับ 50 กม./ชม.

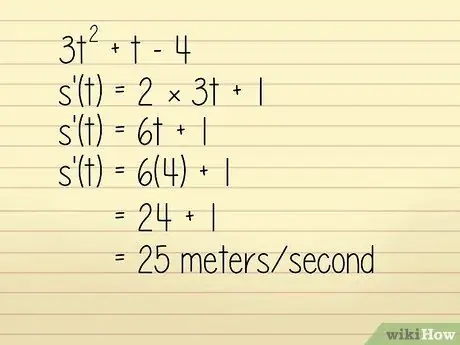
ขั้นตอนที่ 3 หาอนุพันธ์ของตำแหน่งของฟังก์ชัน

หากคุณมีฟังก์ชัน k(w) ที่แสดงตำแหน่งของวัตถุโดยไม่ต้องคำนวณเวลา อนุพันธ์ของ k(w) จะแสดงความเร่งโดยไม่จำเป็นต้องจับเวลา เพียงเสียบค่าเวลาลงในสูตรนี้เพื่อให้ตัวแปร w (หรือค่าเวลาใดก็ตามที่ใช้) ถูกเร่งตามเวลานั้น จากที่นี่ คุณสามารถค้นหาความเร็วของวัตถุได้อย่างง่ายดาย

• ตัวอย่างเช่น สมมติว่าตำแหน่งของวัตถุในหนึ่งเมตรอธิบายไว้ในสมการ 3q² + w - 4 โดยที่ w = เวลาเป็นวินาที เราต้องการทราบความเร็วของวัตถุที่ w = 4 วินาที ในกรณีนี้ คุณสามารถแก้ไขได้โดย:

  3w² +w - 4

  k'(w) = 2 × 3w + 1

  k'(w) = 6w + 1

• ตอนนี้เราป้อน w = 4:

  k'(w) = 6(4) + 1 = 24 + 1 = 25 เมตร/วินาที. ในทางเทคนิคแล้ว นี่คือการคำนวณความเร่ง แต่เนื่องจากเป็นค่าบวกและไม่มีการระบุทิศทางในคำถาม เราจึงสามารถใช้มันเพื่อค้นหาความเร็วได้

ขั้นตอนที่ 4 ใช้ฟังก์ชันการเร่งความเร็วอินทิกรัล

ความเร่งเป็นวิธีการวัดการเปลี่ยนแปลงความเร่งของวัตถุในช่วงเวลาหนึ่ง หัวข้อนี้ซับซ้อนเกินกว่าจะอธิบายอย่างครบถ้วนในบทความนี้ อย่างไรก็ตาม ควรสังเกตว่าเมื่อคุณมีฟังก์ชัน a(w) ที่แสดงถึงความเร่งเทียบกับเวลา ปริพันธ์ของ a(w) จะคืนค่าผลลัพธ์ของการเร่งตามเวลานั้น จำไว้ว่า มันมีประโยชน์มากที่จะรู้ความเร่งเริ่มต้นของวัตถุ เพื่อที่คุณจะได้กำหนดค่าคงที่ของผลลัพธ์นั้นจากอินทิกรัลอนันต์

• ตัวอย่างเช่น สมมติว่าวัตถุมีความเร่งคงที่ (เป็น m/s² เป็นผลมาจาก a(w) = -30 กล่าวอีกอย่างว่าวัตถุมีความเร่งเริ่มต้นที่ 10 m/s เราต้องหาความเร็วที่ w = 12 วินาที ในกรณีนี้ เราสามารถแก้ไขได้โดย:

  a(w) = -30

  p(w)= a(w)dw = -30dw = -30w + C

• ในการหา C เราจะแก้ p(w) สำหรับ w = 0 จำไว้ว่าความเร่งเริ่มต้นของวัตถุคือ 10 m/s

  p(0) = 10 = -30(0) + C

  10 = C ดังนั้น p(w) = -30w + 10

• ตอนนี้ เราสามารถป้อน w = 12 วินาที

  p(12) = -30(12) + 10 = -360 + 10 = -350 เนื่องจากความเร็วเป็นค่าความเร่งสัมบูรณ์ ความเร็วของวัตถุจึงเท่ากับ 350 เมตร/วินาที.

เคล็ดลับ

• การฝึกฝนทำให้ยอดเยี่ยม! ลองสร้างคำถามของคุณเองโดยแทนที่ตัวเลขในปัญหาตัวอย่างด้านบน
• หากคุณกำลังมองหาวิธีที่รวดเร็วในการฝึกแคลคูลัสเพื่อความเร็วในการคำนวณที่ดีขึ้น ให้ใช้เครื่องคำนวณอนุพันธ์ออนไลน์ที่นี่และเครื่องคิดเลขอินทิกรัลออนไลน์ที่นี่