- ผู้เขียน Jason Gerald [email protected].
- Public 2024-01-15 08:25.
- แก้ไขล่าสุด 2025-01-23 12:49.
มีหลายวิธีที่จะทำการแบ่ง คุณสามารถหารทศนิยม เศษส่วน หรือแม้แต่เลขชี้กำลัง และใช้การหารยาวหรือสั้นได้ หากคุณต้องการทราบวิธีการหารตัวเลขแบบต่างๆ ให้ทำตามขั้นตอนด้านล่าง
ขั้นตอน
วิธีที่ 1 จาก 5: การดำเนินการกองอนุกรมยาว

ขั้นตอนที่ 1 เขียนคำถาม
ในการหารยาว ให้วางตัวส่วน (ตัวเลขที่จะหาร) นอกแถบตัวหาร และตัวเศษ (ตัวเลขที่จะหาร) ข้างในแถบตัวหาร
ตัวอย่างเช่น: 136÷3

ขั้นตอนที่ 2 แบ่งหลักแรกของตัวเศษด้วยตัวส่วน (ถ้าเป็นไปได้)
ในตัวอย่างนี้ 1 ไม่สามารถหารด้วย 3 ลงตัว ดังนั้นให้ใส่ 0 เหนือแถบตัวหารและไปยังขั้นตอนถัดไป ลบ 1 ด้วย 0 และใส่ผลลัพธ์ไว้ใต้หมายเลข 1

ขั้นตอนที่ 3 หารจำนวนเศษของหลักแรกของตัวเศษและหลักที่สองของตัวเศษด้วยตัวส่วน
เนื่องจาก 1 ไม่สามารถหารด้วย 3 ได้ จึงยังคงใช้เลข 1 อยู่ คุณต้องลบ 3 ทีนี้ หาร 13 ด้วย 3 เนื่องจาก 3 x 4 = 12 ให้วาง 4 ไว้เหนือแถบตัวหาร (ทางด้านขวาของ 0) จากนั้นลบ 13 ด้วย 12 แล้วเขียนผลลัพธ์ด้านล่าง

ขั้นตอนที่ 4 หารตัวเลขที่เหลือด้วยตัวส่วน
ลดเลข 6 ไปทางขวาของ 1 เพื่อให้ได้ 16 ทีนี้ หาร 16 ด้วย 3 เนื่องจาก 3 x 5 = 15 ให้เขียนเลข 5 ทางด้านขวาของตัวเลข 4 แล้วลบ 16 ด้วย 15 แล้วเขียนผลลัพธ์ (16-15= 1) ด้านล่างครับ

ขั้นตอนที่ 5. เขียนส่วนที่เหลือถัดจากผลหาร
คำตอบสุดท้ายของคุณคือ 45 โดยเหลือ 1 รายการหรือ 45 R1
วิธีที่ 2 จาก 5: การดำเนินการส่วนสั้น

ขั้นตอนที่ 1 เขียนคำถาม
เขียนตัวส่วน (ตัวเลขที่จะหาร) นอกแถบตัวหาร และตัวเศษ (ตัวเลขที่จะหาร) ภายในแถบตัวหาร โปรดทราบว่าในการหารสั้น ตัวส่วนต้องไม่เกินหนึ่งหลัก
ตัวอย่างเช่น 518 4

ขั้นตอนที่ 2 หารหลักแรกของตัวเศษด้วยตัวส่วน
5 4 = 1 R1 วางผลหาร (1) เหนือแถบตัวแบ่งยาว เขียนเศษที่เหลือเหนือหลักแรกของตัวเศษ วาง 1 ส่วน 5 เล็กๆ เพื่อเตือนคุณว่าคุณมี 1 เหลือเมื่อคุณหาร 5 ด้วย 4 ตอนนี้ 518 ควรมีลักษณะดังนี้: 5118

ขั้นตอนที่ 3 หารจำนวนที่เกิดขึ้นจากเศษที่เหลือและหลักที่สองของตัวเศษด้วยตัวส่วน
ตัวเลขถัดไปคือ 11 ซึ่งได้มาจากมูลค่าคงเหลือ (1) และหลักที่สองของตัวเศษ (1) 11 4 = 2 R 3 เพราะ 4 x 2 = 8 เหลือเศษ 3 เขียนค่าคงเหลือเหนือหลักที่สองของตัวเศษ ใส่ 3 ส่วน 1 ตัวเศษเริ่มต้น (518) ตอนนี้มีลักษณะดังนี้: 51138

ขั้นตอนที่ 4 หารตัวเลขที่เหลือด้วยตัวส่วน
จำนวนที่เหลือคือ 38; ตัวเลข 3 มาจากส่วนที่เหลือของสเตจก่อนหน้า และ 8 คือหลักสุดท้ายของตัวเศษ คำนวณ 38 4 = 9 R2 เนื่องจาก 4 x 9 = 36 ให้เขียน "R2" เหนือแถบหารเพราะ 38 - 36 = 2

ขั้นตอนที่ 5. เขียนคำตอบสุดท้าย
ผลลัพธ์สุดท้ายและผลหารอยู่เหนือแถบตัวหาร คำตอบคือ 518 4 = 129 R2
วิธีที่ 3 จาก 5: หารเศษส่วน

ขั้นตอนที่ 1 เขียนคำถาม
ในการหารเศษส่วน ให้เขียนเศษส่วนแรกตามด้วยสัญลักษณ์หารแล้วตามด้วยเศษส่วนที่สอง
ตัวอย่างเช่น: 3/4 5/8

ขั้นตอนที่ 2 กลับตัวเศษและตัวส่วนของเศษส่วนที่สอง
เศษส่วนที่สองตอนนี้เป็นส่วนกลับ
ตัวอย่าง: 3/4 8/5

ขั้นตอนที่ 3 เปลี่ยนสัญลักษณ์หารเป็นสัญลักษณ์เวลา
ในการหารเศษส่วน คุณต้องคูณเศษส่วนแรกด้วยส่วนกลับของส่วนที่สอง
ตัวอย่าง: 3/4 x 8/5
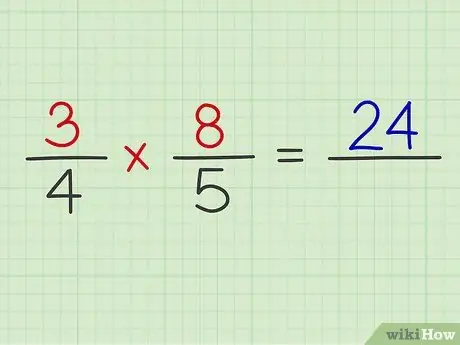
ขั้นตอนที่ 4 คูณตัวเศษของเศษส่วนทั้งสอง
ทำเหมือนการคูณเศษส่วนธรรมดาสองส่วน.
ตัวอย่าง: 3 x 8 = 24
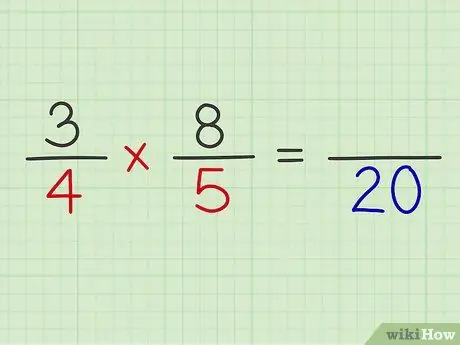
ขั้นตอนที่ 5. คูณตัวส่วนของเศษส่วนทั้งสอง
ทำการคำนวณโดยคูณเศษส่วนสองส่วน
ตัวอย่าง: 4 x 5 = 20
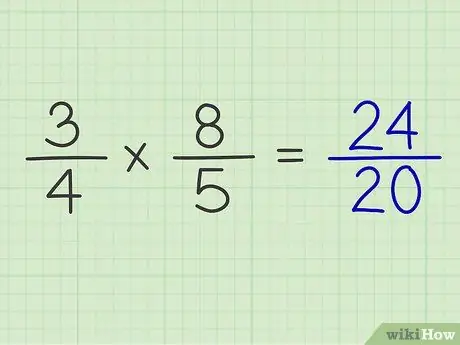
ขั้นตอนที่ 6. วางผลคูณของตัวเศษไว้เหนือผลคูณของตัวส่วน
หลังจากคูณทั้งตัวเศษและตัวส่วนของเศษส่วนทั้งสองแล้ว คุณจะได้ผลลัพธ์จากการคำนวณเศษส่วนทั้งสอง
ตัวอย่าง: 3/4 x 8/5 = 24/20

ขั้นตอนที่ 7 ลดความซับซ้อนของเศษส่วน
เพื่อหาตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดหรือจำนวนที่มากที่สุดที่หารตัวเศษและตัวส่วนเท่า ๆ กัน ในกรณีนี้ ตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดของ 24 และ 20 คือ 4 ในการพิสูจน์ ให้เขียนตัวเศษและตัวส่วนทั้งหมด แล้ววงกลมจำนวนตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดของทั้งสอง
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- เนื่องจาก 4 เป็นตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดของ 24 และ 20 เพียงแค่หารตัวเลขทั้งสองด้วย 4 เพื่อทำให้เศษส่วนง่ายขึ้น
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

ขั้นตอนที่ 8 เขียนเศษส่วนใหม่เป็นจำนวนคละ (ไม่บังคับ)
เคล็ดลับ แค่หารตัวเศษด้วยตัวส่วน แล้วเขียนผลลัพธ์เป็นจำนวนเต็ม หลังจากนั้นให้เขียนเศษที่เหลือเป็นตัวเศษใหม่ และตัวส่วนของเศษส่วนจะไม่เปลี่ยนแปลง เนื่องจาก 6 หารด้วย 5 ผลลัพธ์ใน 1 กับเศษ 1 ให้เขียนจำนวนเต็ม 1 ตามด้วยตัวเศษ 1 ใหม่ แล้วตัวส่วน 5 เพื่อให้ได้จำนวนคละ 1 1/5
ตัวอย่าง: 6/5 = 1 1/5
วิธีที่ 4 จาก 5: หารเลขยกกำลัง

ขั้นตอนที่ 1. ตรวจสอบให้แน่ใจว่าเลขชี้กำลัง/กำลังมีเลขฐานเหมือนกัน
คุณสามารถหารเลขชี้กำลังได้ก็ต่อเมื่อมีเลขฐานเท่ากัน มิฉะนั้น คุณสามารถลองจัดการมันจนกว่าคุณจะได้เลขฐานเดียวกัน
ตัวอย่าง: x8 NS5

ขั้นตอนที่ 2 ลบเลขชี้กำลัง
คุณก็แค่ลบเลขชี้กำลังแรกด้วยตัวที่สอง อย่าเพิ่งสนใจตัวเลขฐานในตอนนี้
ตัวอย่าง: 8 - 5 = 3
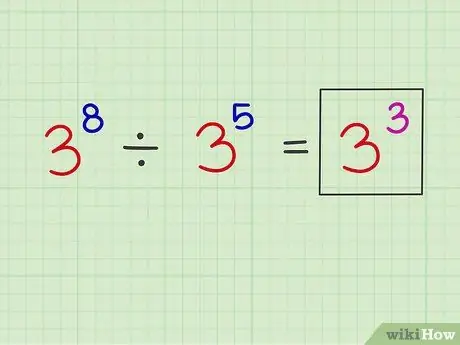
ขั้นตอนที่ 3 วางเลขชี้กำลังใหม่เหนือเลขฐานเดิม
ตอนนี้คุณสามารถเขียนเลขชี้กำลังใหม่ทับเลขฐานเดิมได้
ตัวอย่าง: x8 NS5 = x3
วิธีที่ 5 จาก 5: การหารเลขทศนิยม

ขั้นตอนที่ 1 เขียนคำถาม
เขียนตัวส่วน (ตัวเลขที่จะหาร) นอกแถบตัวหาร และตัวเศษ (ตัวเลขที่จะหาร) ภายในแถบตัวหาร ในการหารทศนิยม เป้าหมายของคุณคือการแปลงเลขทศนิยมให้เป็นจำนวนเต็ม
ตัวอย่าง: 65.5.5

ขั้นตอนที่ 2 เปลี่ยนตัวส่วนเป็นจำนวนเต็ม
เพียงเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักเพื่อเปลี่ยน 0.5 เป็น 5 หรือที่รู้จักว่า 5, 0

ขั้นตอนที่ 3 เปลี่ยนตัวเศษโดยเลื่อนจุดทศนิยมด้วยจำนวนหลักเดียวกับตัวส่วน
เนื่องจากคุณย้ายจุดทศนิยมของตัวเศษไปทางขวาหนึ่งหลักเพื่อให้กลายเป็นจำนวนเต็ม จุดทศนิยมของตัวส่วนจึงเลื่อนไปทางขวาหนึ่งหลักเพื่อให้ 65.5 เปลี่ยนเป็น 655
หากคุณเลื่อนจุดทศนิยมของตัวเศษเกินกว่าตัวเลขทั้งหมด หมายความว่าคุณต้องเพิ่มศูนย์ให้กับตัวเลขทุกครั้งที่เปลี่ยนจุดทศนิยม ตัวอย่างเช่น ถ้าจุดทศนิยม 7, 2 ถูกเลื่อนไปทางขวาสามหลัก ตัวเลขจะเปลี่ยนเป็น 7,200 เนื่องจากช่องว่างสองหลักเต็มไปด้วยศูนย์

ขั้นตอนที่ 4 วางจุดทศนิยมบนแถบหารยาวเหนือจุดทศนิยมในตัวเศษ
เนื่องจากคุณกำลังเลื่อนจุดทศนิยมหนึ่งหลักเพื่อให้ 0.5 เป็นจำนวนเต็ม จึงเป็นความคิดที่ดีที่จะวางจุดทศนิยมเหนือแถบการหารตรงตำแหน่งที่จุดทศนิยมถูกเลื่อน กล่าวคือ หลังจาก 5 สุดท้ายใน 655

ขั้นตอนที่ 5. แก้ปัญหาด้วยการหารยาวอย่างง่าย
ในการหาร 655 ด้วย 5 มีขั้นตอนดังนี้
- หารหลักร้อยของตัวเศษ (6) ด้วยตัวส่วน (5) ผลลัพธ์คือ 1 โดยเหลือ 1 เขียนตัวเลข 1 เหนือแถบตัวหาร และเขียน 5 ใต้ตัวเลข 6 ที่จะลบออก
- เศษ 1 ที่เหลือถูกลบออกจากหลักสิบของตัวเศษ (5) คุณจะได้ 15 หาร 15 ด้วย 5 เพื่อให้ได้ 3 เขียน 3 เหนือแถบตัวหาร ทางด้านขวาของ 1
- ทิ้ง 5 หลักสุดท้าย. หาร 5 ด้วย 5 เพื่อให้ได้ 1 เขียนเลข 1 ไว้บนแถบตัวหาร ทางด้านขวาของตัวเลข 3 ไม่มีเศษเหลือเพราะ 5 หารด้วย 5 ลงตัว
- คำตอบการหารแบบต่อเนื่องแบบยาวคือ 655 5 = 131 ผลลัพธ์นี้เหมือนกับคำตอบของคำถาม 65.5 0.5

