- ผู้เขียน Jason Gerald [email protected].
- Public 2024-02-01 14:16.
- แก้ไขล่าสุด 2025-01-23 12:48.
การกระจัดในฟิสิกส์แสดงถึงการเปลี่ยนแปลงในตำแหน่งของวัตถุ เมื่อคุณคำนวณการกระจัด คุณจะคำนวณว่าวัตถุอยู่ห่างจากตำแหน่งเริ่มต้นและตำแหน่งสุดท้ายเท่าใด สูตรที่คุณใช้คำนวณการกระจัดขึ้นอยู่กับตัวแปรที่กำหนดให้กับปัญหา ทำตามขั้นตอนเหล่านี้เพื่อคำนวณการกระจัด
ขั้นตอน
ส่วนที่ 1 จาก 5: การคำนวณการกระจัดผลลัพธ์

ขั้นตอนที่ 1 ใช้สูตรการกระจัดที่เป็นผลลัพธ์ ถ้าหน่วยของระยะทางถูกใช้เพื่อระบุจุดเริ่มต้นและจุดสิ้นสุดของคุณ
แม้ว่าระยะทางจะแตกต่างจากการกระจัด แต่ปัญหาการกระจัดที่เกิดขึ้นจะพิจารณาว่าวัตถุเดินทางกี่กิโลเมตรหรือเมตร คุณจะใช้หน่วยวัดนี้ในการคำนวณการกระจัดและตำแหน่งของวัตถุเบี่ยงเบนไปจากจุดเริ่มต้นมากน้อยเพียงใด
- สูตรการกระจัดผลลัพธ์เขียนเป็น: S = x²+y². S คือการกระจัด X คือทิศทางแรกของการเคลื่อนที่ของวัตถุ และ Y คือทิศทางที่สองของการเคลื่อนที่ของวัตถุ หากวัตถุของคุณเคลื่อนที่ในทิศทางเดียวเท่านั้น Y = 0
- วัตถุสามารถเคลื่อนที่ได้ไม่เกินสองทิศทางเท่านั้น เนื่องจากการเคลื่อนที่ไปตามแกนเหนือ/ใต้ หรือตะวันออก/ตะวันตกถือเป็นการเคลื่อนที่ที่เป็นกลาง

ขั้นตอนที่ 2 เชื่อมต่อจุดตามลำดับการเคลื่อนไหวและติดป้ายกำกับจาก A-Z
ใช้ไม้บรรทัดวาดเส้นตรงจากจุดหนึ่งไปยังอีกจุดหนึ่ง
- อย่าลืมเชื่อมต่อจุดเริ่มต้นกับจุดสิ้นสุดโดยใช้เส้นตรง นี่คือการกระจัดที่เราจะคำนวณ
- ตัวอย่างเช่น หากวัตถุเคลื่อนที่ไปทางทิศตะวันออก 300 ม. และทิศเหนือ 400 ม. วัตถุนั้นจะกลายเป็นสามเหลี่ยมมุมฉาก AB จะเป็นขาแรกของสามเหลี่ยม และ BC จะเป็นขาที่สอง AC จะเป็นด้านตรงข้ามมุมฉากของสามเหลี่ยมและขนาดของมันคือการกระจัดของวัตถุ ในตัวอย่างนี้ สองทิศทางคือทิศตะวันออกและทิศเหนือ

ขั้นตอนที่ 3 ป้อนค่าสำหรับx²และy²
เมื่อคุณทราบทิศทางการเคลื่อนที่สองทิศทางของวัตถุแล้ว ให้ป้อนค่าลงในตัวแปรที่เหมาะสม
ตัวอย่างเช่น x = 300 และ y = 400 สูตรของคุณควรมีลักษณะดังนี้: S = 300² + 400²
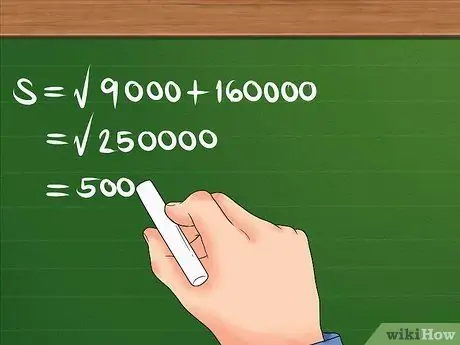
ขั้นตอนที่ 4 คำนวณสูตรโดยใช้ลำดับการดำเนินการ
ยกกำลังสอง 300 กับ 400 ก่อน แล้วบวกกัน แล้วหารากที่สองของผลรวม
ตัวอย่างเช่น: S = 90000 + 160000 S = 250000 S = 500 ตอนนี้คุณรู้แล้วว่าการกระจัดคือ 500 ม
ส่วนที่ 2 จาก 5: เมื่อรู้ความเร็วและเวลา

ขั้นตอนที่ 1 ใช้สูตรนี้เมื่อปัญหาบอกคุณถึงความเร็วของวัตถุและเวลาที่ใช้
ปัญหาทางคณิตศาสตร์บางอย่างไม่ได้บอกคุณว่าวัตถุเคลื่อนที่ได้ไกลหรือเร็วแค่ไหน คุณสามารถคำนวณการกระจัดโดยใช้เวลาและความเร็วขนาดนี้
-
ในกรณีนี้ สูตรจะกลายเป็น: S = 1/2(u + v)t
U = ความเร็วต้นของวัตถุ หรือความเร็วของวัตถุที่เริ่มเคลื่อนที่ไปในทิศทางใดทิศทางหนึ่ง V = ความเร็วสุดท้ายของวัตถุ หรือความเร็วของวัตถุที่เคลื่อนที่ไปยังตำแหน่งสุดท้าย T = เวลาที่วัตถุไปถึงตำแหน่งสุดท้าย
- ตัวอย่าง: รถแล่นไปตามถนนเป็นเวลา 45 วินาที (ต้องใช้เวลา) รถกำลังเลี้ยวไปทางทิศตะวันตกด้วยความเร็ว 20 ม./วินาที (ความเร็วเริ่มต้น) และสุดถนน ความเร็ว 23 ม./วินาที (ความเร็วสุดท้าย) คำนวณการกระจัดตามปัจจัยเหล่านี้

ขั้นตอนที่ 2 ป้อนความเร็วและเวลาที่ต้องการลงในตัวแปรที่เหมาะสม
เมื่อคุณทราบแล้วว่ารถเคลื่อนที่ได้ไกลแค่ไหน รถเคลื่อนที่เร็วแค่ไหนที่จุดเริ่มต้นและจุดสิ้นสุด คุณสามารถค้นหาระยะทางจากตำแหน่งเริ่มต้นไปยังตำแหน่งสุดท้ายได้
สูตรของคุณควรมีลักษณะดังนี้: S = 1/2(20 + 23)45

ขั้นตอนที่ 3 คำนวณสูตรหลังจากที่คุณใส่ค่าในตำแหน่งที่ถูกต้อง
อย่าลืมทำตามลำดับการทำงาน มิฉะนั้น การกระจัดจะส่งผลให้ค่าต่างกันมาก
- สำหรับสูตรนี้ ไม่สำคัญว่าคุณจะสลับความเร็วเริ่มต้นและสิ้นสุดโดยไม่ได้ตั้งใจหรือไม่ เนื่องจากคุณจะรวมตัวเลขเหล่านี้เข้าด้วยกันก่อน จึงไม่สำคัญว่าตัวเลขเหล่านั้นจะอยู่ที่ใดในวงเล็บ อย่างไรก็ตาม สำหรับสูตรอื่นๆ การสลับความเร็วเริ่มต้นและความเร็วสุดท้ายจะทำให้ค่าการกระจัดต่างกัน
- สูตรของคุณควรมีลักษณะดังนี้: S = 1/2(43)45 ขั้นแรกให้หาร 43 ด้วย 2 ซึ่งได้ผลลัพธ์เป็น 21, 5 จากนั้นคูณ 21, 5 ด้วย 45 ดังนั้นผลลัพธ์ที่ได้คือ 967.5 เมตร 967, 5 คือขนาดของการกระจัดของคุณ หรือระยะที่รถของคุณเคลื่อนจากจุดเริ่มต้น
ตอนที่ 3 จาก 5: เมื่อรู้ความเร็ว ความเร่ง และเวลาเริ่มต้น
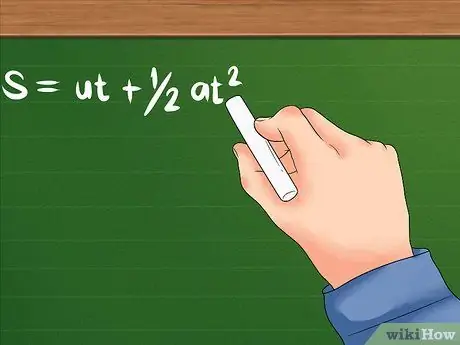
ขั้นตอนที่ 1 ใช้สูตรที่แก้ไขเมื่อทราบความเร่งนอกเหนือจากความเร็วและเวลาเริ่มต้น
คำถามบางข้อจะบอกคุณแค่ว่าวัตถุเคลื่อนที่เร็วแค่ไหนในตอนเริ่มต้น วัตถุเริ่มเร่งความเร็วเร็วแค่ไหน และวัตถุเคลื่อนที่ได้ไกลแค่ไหน คุณจะต้องใช้สูตรต่อไปนี้
- สูตรสำหรับปัญหานี้คือ: S = ut + 1/2at². คุณยังคงระบุความเร็วเริ่มต้น a คือความเร่งของวัตถุหรือความเร็วของวัตถุเริ่มเปลี่ยนแปลงเร็วเพียงใด T อาจหมายถึงเวลาที่ใช้หรือระยะเวลาหนึ่งที่วัตถุใช้ในการเร่งความเร็ว ทั้งสองจะใช้หน่วยเวลา เช่น วินาที ชั่วโมง และอื่นๆ
- สมมติว่ารถเคลื่อนที่ด้วยความเร็ว 25 m/s (ความเร็วเริ่มต้น) เริ่มเร่งความเร็วที่ 3 m/s2 (อัตราเร่ง) เป็นเวลา 4 วินาที (เวลา) การกระจัดของรถหลังจาก 4 วินาทีคืออะไร?

ขั้นตอนที่ 2 ป้อนค่าในสูตร
ต่างจากสูตรก่อนหน้านี้ คือ แสดงเฉพาะความเร็วเริ่มต้นที่นี่ ดังนั้นโปรดป้อนข้อมูลที่ถูกต้อง
จากข้อมูลตัวอย่างข้างต้น สูตรของคุณจะมีลักษณะดังนี้: S = 25(4) + 1/2(3)4² ช่วยเพิ่มวงเล็บรอบขนาดความเร่งและเวลาของคุณเพื่อช่วยในการแยกตัวเลข
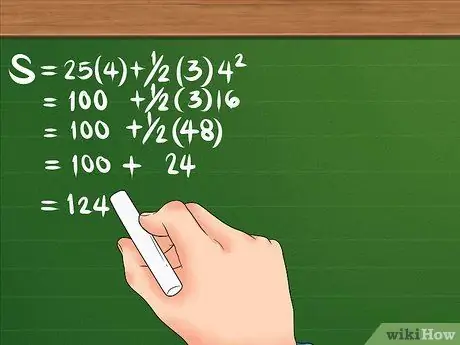
ขั้นตอนที่ 3 คำนวณการกระจัดโดยทำตามลำดับการดำเนินการที่ถูกต้อง
วิธีที่รวดเร็วที่จะช่วยให้คุณจำลำดับการดำเนินการได้คือสะพานลา Kur ir Kua ci Kadang Ba wa Juragan Turtles ซึ่งแสดงถึงลำดับที่ถูกต้อง ได้แก่ วงเล็บ สี่เหลี่ยม คูณ หาร บวก และลบ
ลองดูสูตรอีกครั้ง: S = 25(4) + 1/2(3)4² อย่างแรก สี่เหลี่ยม 4 ผลลัพธ์คือ 16 จากนั้นคูณ 16 ด้วย 3 ได้ 48 จากนั้นคูณ 25 ด้วย 4 เพื่อให้ได้ 100 หาร 48 ด้วย 2 ได้ 24 สมการของคุณควรมีลักษณะดังนี้: S = 100 + 24 เมื่อคุณบวกทั้งสองเข้าด้วยกัน การกระจัดคือ 124 เมตร
ส่วนที่ 4 จาก 5: การคำนวณการกระจัดเชิงมุม

ขั้นตอนที่ 1 ค้นหาการกระจัดเชิงมุมเมื่อวัตถุเคลื่อนที่เป็นเส้นทางวงกลม
แม้ว่าคุณจะยังคงคำนวณการกระจัดโดยใช้เส้นตรง คุณจะต้องค้นหาความแตกต่างระหว่างตำแหน่งเริ่มต้นและจุดสิ้นสุดของวัตถุขณะที่เคลื่อนที่เป็นเส้นทางวงกลม
- ลองนึกภาพเด็กผู้หญิงนั่งบนม้าหมุน เมื่อเขาหมุนด้วยม้าหมุน เขาจะเคลื่อนที่เป็นวงกลม การกระจัดเชิงมุมพยายามค้นหาระยะทางที่สั้นที่สุดระหว่างตำแหน่งเริ่มต้นและตำแหน่งสุดท้ายเมื่อวัตถุไม่เคลื่อนที่เป็นเส้นตรง
- สูตรสำหรับการกระจัดเชิงมุมคือ: = S/r โดยที่ S คือการกระจัดเชิงเส้น r คือรัศมี และคือการกระจัดเชิงมุม การกระจัดเชิงเส้นคือระยะที่วัตถุเคลื่อนที่ไปตามส่วนโค้ง รัศมีคือระยะห่างของวัตถุถึงจุดศูนย์กลางของวงกลม การกระจัดเชิงมุมคือค่าที่เราต้องการหา

ขั้นตอนที่ 2 เสียบการกระจัดเชิงเส้นและรัศมีลงในสมการ
จำไว้ว่ารัศมีคือระยะห่างจากจุดศูนย์กลางของวงกลม ปัญหาบางอย่างจะบอกคุณถึงเส้นผ่านศูนย์กลางของวงกลม ซึ่งต้องหารด้วย 2 เพื่อหารัศมี
- นี่คือตัวอย่างปัญหา: เด็กผู้หญิงขี่ม้าม้าหมุน เบาะนั่งอยู่ห่างจากจุดศูนย์กลางวงกลม (รัศมี) 1 เมตร หากหญิงสาวเคลื่อนที่ในวิถีโค้ง 1.5 เมตร (การกระจัดเชิงเส้น) การกระจัดเชิงมุมของเธอคืออะไร?
- สมการของคุณจะมีลักษณะดังนี้: = 1.5/1
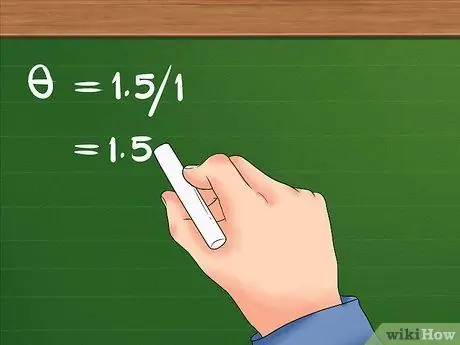
ขั้นตอนที่ 3 แบ่งการกระจัดเชิงเส้นด้วยรัศมี
การหารนี้จะส่งผลให้เกิดการเคลื่อนตัวเชิงมุมของวัตถุ
- หลังจากหาร 1.5 ด้วย 1 ผลลัพธ์ที่ได้คือ 1.5 การกระจัดเชิงมุมของหญิงสาวเท่ากับ 1.5 เรเดียน
- เนื่องจากการกระจัดเชิงมุมจะวัดว่าวัตถุหมุนจากตำแหน่งเริ่มต้นมากเพียงใด จึงควรวัดเป็นมุม ไม่ใช่ระยะทาง เรเดียนเป็นหน่วยที่ใช้วัดมุม
ส่วนที่ 5 จาก 5: ความเข้าใจเกี่ยวกับการโยกย้ายถิ่นฐาน
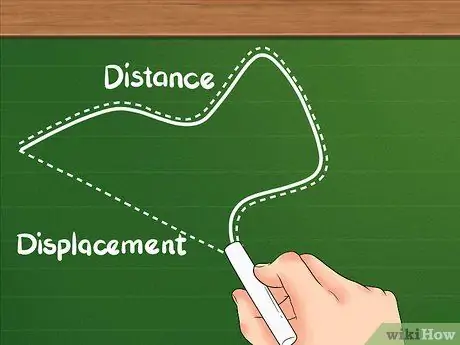
ขั้นตอนที่ 1. รู้ว่าระยะทางมีคำจำกัดความที่แตกต่างจากการกระจัด
ระยะทางแสดงระยะทางทั้งหมดที่วัตถุเดินทาง
- ระยะทางมักเรียกว่าปริมาณสเกลาร์ Distance แสดงระยะทางที่วัตถุเคลื่อนที่โดยไม่คำนึงถึงทิศทางของวัตถุ
- ตัวอย่างเช่น หากคุณเดิน 2 ก้าวไปทางตะวันออก 2 ก้าวใต้ 2 ก้าวไปทางตะวันตก และ 2 ก้าวไปทางเหนือ คุณจะกลับสู่ตำแหน่งเริ่มต้น แม้จะผ่านเกณฑ์มาครบ ระยะทาง ห่างไป 10 ก้าว คุณก็แค่ เคลื่อนไหว ห่างออกไป 0 ก้าว เนื่องจากตำแหน่งสุดท้ายของคุณเหมือนกับตำแหน่งเริ่มต้น (เส้นทางของคุณคล้ายกับกล่อง)

ขั้นตอนที่ 2 ทำความเข้าใจว่าการกระจัดเป็นความแตกต่างระหว่างสถานที่สองแห่ง
การกระจัดไม่ใช่ผลรวมของการเคลื่อนที่เหมือนระยะทาง กะจะเน้นที่พื้นที่ระหว่างจุดเริ่มต้นและจุดสิ้นสุดของคุณ
- การกระจัดเรียกว่าปริมาณเวกเตอร์และแสดงการเปลี่ยนแปลงในตำแหน่งของวัตถุโดยพิจารณาจากทิศทางการเคลื่อนที่ของวัตถุ
- ตัวอย่างเช่น คุณเดินไปทางทิศตะวันออก 5 ก้าว หากคุณย้อนกลับไปทางทิศตะวันตก 5 ก้าว คุณจะเคลื่อนที่ไปในทิศทางตรงกันข้ามจากตำแหน่งเดิมของคุณ แม้ว่าคุณจะครอบคลุม 10 ขั้นตอนแล้ว ตำแหน่งของคุณก็ไม่เปลี่ยนแปลง การกระจัดของคุณคือ 0 ขั้นตอน

ขั้นตอนที่ 3 จำคำศัพท์ไปข้างหน้าและข้างหลังเมื่อพยายามจินตนาการถึงการกระจัด
การเคลื่อนที่ไปในทิศทางตรงกันข้ามช่วยลดการกระจัดของวัตถุ
ลองนึกภาพโค้ชทีมฟุตบอลที่อยู่ข้างสนาม ขณะที่เขาตะโกนใส่ผู้เล่น เขาขยับจากซ้ายไปขวาหลายครั้ง หากคุณดูเขาขณะที่เขาเคลื่อนที่จากซ้ายไปขวา แสดงว่าคุณสังเกตระยะทางทั้งหมดที่เขาเดินทาง อย่างไรก็ตาม สมมติว่าโค้ชหยุดคุยกับกองหลังข้างสนาม หากเขาอยู่ที่จุดต่างจากตำแหน่งเดิมก่อนที่จะเคลื่อนไหว แสดงว่าคุณกำลังสังเกตการเคลื่อนไหวของผู้ฝึกสอน

ขั้นตอนที่ 4 รู้ว่าการกระจัดนั้นวัดโดยใช้เส้นทางตรง ไม่ใช่เส้นทางวงกลม
ในการหาการกระจัด คุณต้องหาวิธีที่สั้นที่สุดและมีประสิทธิภาพมากที่สุดในการคำนวณความแตกต่างระหว่างจุดสองจุด
- เส้นทางวงกลมจะนำคุณจากตำแหน่งเริ่มต้นไปยังตำแหน่งสุดท้าย แต่ไม่ใช่เส้นทางที่สั้นที่สุด เพื่อช่วยให้คุณเห็นภาพได้ ให้จินตนาการว่าคุณกำลังเดินเป็นเส้นตรงและเจอเสา คุณไม่สามารถเจาะทะลุเสานี้ได้ ดังนั้นคุณต้องเดินไปรอบๆ แม้ว่าตำแหน่งสุดท้ายของคุณจะเหมือนกับว่าคุณฝ่าเสาหลักได้ แต่คุณจะต้องทำตามขั้นตอนเพิ่มเติมเพื่อบรรลุเป้าหมายนั้น
- แม้ว่าการกระจัดเป็นตัวแทนของเส้นทางตรง แต่ให้รู้ว่าคุณสามารถวัดการกระจัดของวัตถุที่เป็น ตอนนี้ เคลื่อนที่เป็นวงกลม การกระจัดนี้เรียกว่าการกระจัดเชิงมุมและสามารถคำนวณได้โดยการหาเส้นทางที่สั้นที่สุดจากตำแหน่งเริ่มต้นไปยังตำแหน่งสุดท้าย

ขั้นตอนที่ 5. รู้ว่าการกระจัดอาจเป็นค่าลบ ไม่เหมือนระยะทาง
หากไปถึงตำแหน่งสุดท้ายของคุณโดยการเคลื่อนที่ไปในทิศทางตรงกันข้ามกับทิศทางเริ่มต้น การกระจัดของคุณจะเป็นลบ
- ตัวอย่างเช่น เราเดิน 5 ก้าวไปทางตะวันออก และ 3 ก้าวไปทางทิศตะวันตก แม้ว่าคุณจะย้าย 2 ขั้นตอนจากตำแหน่งเริ่มต้นโดยการคำนวณ การกระจัดของคุณคือ -2 เนื่องจากคุณกำลังเคลื่อนที่ไปในทิศทางตรงกันข้าม ระยะทางของคุณจะเป็นบวกเสมอ เพราะคุณไม่สามารถนับถอยหลังเป็นก้าว กิโลเมตร และอื่นๆ ได้
- การกระจัดเชิงลบไม่ได้หมายความว่าการกระจัดลดลง ค่าลบหมายถึงทิศทางตรงกันข้าม

ขั้นตอนที่ 6 ตระหนักว่าบางครั้งระยะทางและการกระจัดอาจเท่ากัน
หากคุณเดินตรงไป 25 ขั้นแล้วหยุด ระยะทางที่คุณเดินทางจะเท่ากับระยะเคลื่อนที่จากตำแหน่งเดิมของคุณ
- สิ่งนี้ใช้ได้เฉพาะเมื่อคุณย้ายจากตำแหน่งหนึ่งจากตำแหน่งเริ่มต้นของคุณเป็นเส้นตรงเท่านั้น ตัวอย่างเช่น คุณอาศัยอยู่ในซานฟรานซิสโก แคลิฟอร์เนีย และได้งานใหม่ในลาสเวกัส รัฐเนวาดา คุณต้องย้ายไปลาสเวกัสเพื่อจะได้ใกล้ชิดกับงานของคุณ ถ้าคุณขึ้นเครื่องบินที่บิน ตรง จากซานฟรานซิสโกถึงลาสเวกัส คุณจะเดินทางในระยะทางและระยะทางเท่ากัน x
- อย่างไรก็ตาม หากคุณขับรถจากซานฟรานซิสโกไปลาสเวกัส คุณจะเดินทางเป็นระยะทาง x แต่เดินทางเป็นระยะทาง y เนื่องจากการขับรถมักจะมีทิศทางที่เปลี่ยนแปลงได้ (ทางตะวันออกของถนนสายนี้ ทางตะวันตกของถนนสายนั้น) คุณจะเดินทางในระยะทางที่ไกลกว่าระยะทางที่สั้นที่สุดระหว่างสองเมือง






