วิธีคำนวณ P-Score: 7 ขั้นตอน (พร้อมรูปภาพ)

2024 ผู้เขียน: Jason Gerald | [email protected]. แก้ไขล่าสุด: 2024-01-15 08:25

ค่า P คือการวัดทางสถิติที่ช่วยให้นักวิทยาศาสตร์สามารถระบุได้ว่าสมมติฐานของพวกเขาถูกต้องหรือไม่ ค่า P ใช้เพื่อระบุว่าผลการทดลองอยู่ในช่วงค่าปกติสำหรับสิ่งที่ศึกษาหรือไม่ โดยปกติ หากค่า P ของชุดข้อมูลต่ำกว่าค่าที่กำหนดไว้ล่วงหน้า (เช่น 0.05) นักวิทยาศาสตร์จะปฏิเสธสมมติฐานว่างของการทดลอง กล่าวอีกนัยหนึ่ง พวกเขาจะตัดสมมติฐานที่ตัวแปรทดลองมี ไม่มีผลกระทบอย่างมีนัยสำคัญ ต่อผลลัพธ์ วันนี้ ค่า p มักจะพบในตารางอ้างอิงโดยการคำนวณค่าไคกำลังสอง

ขั้นตอน

ขั้นตอนที่ 1 กำหนดผลลัพธ์ที่คาดหวังจากการทดสอบของคุณ

โดยปกติเมื่อนักวิทยาศาสตร์ทำการทดลองและตรวจสอบผลลัพธ์ พวกเขามีแนวคิดเกี่ยวกับผลลัพธ์ปกติหรือผลปกติล่วงหน้าอยู่แล้ว ซึ่งอาจขึ้นอยู่กับผลของการทดลองครั้งก่อน ชุดข้อมูลเชิงสังเกตที่เชื่อถือได้ เอกสารทางวิทยาศาสตร์ และ/หรือแหล่งข้อมูลอื่นๆ สำหรับการทดสอบของคุณ ให้กำหนดผลลัพธ์ที่คาดหวังและจดไว้เป็นตัวเลข

ตัวอย่าง: สมมติว่าการศึกษาก่อนหน้านี้แสดงให้เห็นว่า ในระดับประเทศ มีการออกตั๋วความเร็วให้รถสีแดงบ่อยกว่ารถสีน้ำเงิน สมมติว่าผลเฉลี่ยในระดับประเทศแสดงอัตราส่วน 2:1 โดยมีอัตราส่วนรถสีแดงมากกว่า เราต้องการทราบว่าตำรวจในเมืองของเรามีแนวโน้มเช่นเดียวกันหรือไม่โดยการวิเคราะห์ตั๋วเร่งที่ออกโดยตำรวจในเมืองของเรา ถ้าเราสุ่มตัวอย่างตั๋วโดยสาร 150 ใบที่แจกให้ทั้งรถสีแดงและสีน้ำเงินในเมืองของเรา เราคงคาดหวังไว้ 100 สำหรับรถสีแดงและ 50 สำหรับรถสีน้ำเงินหากหน่วยตำรวจในเมืองของเราออกตั๋วตามการเปรียบเทียบในระดับชาติ

ขั้นตอนที่ 2 กำหนดข้อสังเกตการทดลองของคุณ

เมื่อคุณได้กำหนดมูลค่าที่คาดหวังแล้ว คุณสามารถทำการทดสอบและค้นหามูลค่าที่แท้จริง (หรือการสังเกต) อีกครั้ง ให้เขียนผลลัพธ์เป็นตัวเลข หากเราจัดการเงื่อนไขการทดลองบางอย่างและผลลัพธ์ที่สังเกตพบแตกต่างจากผลลัพธ์ที่คาดไว้ มีความเป็นไปได้สองอย่าง: สิ่งนี้เกิดขึ้นโดยบังเอิญ หรือเป็นการจัดการตัวแปรทดลองของเราที่ทำให้เกิดความแตกต่างนี้ จุดประสงค์ในการค้นหาค่า p นั้นโดยพื้นฐานแล้วเพื่อพิจารณาว่าผลลัพธ์ที่สังเกตได้นั้นแตกต่างจากผลลัพธ์ที่คาดหวังจนถึงจุดที่สมมติฐานว่างหรือไม่ – สมมติฐานที่ว่าไม่มีความสัมพันธ์ระหว่างตัวแปรทดลองกับผลลัพธ์ที่สังเกตได้นั้นไม่สามารถปฏิเสธได้

ตัวอย่าง: สมมุติว่าในเมืองของเรา เราสุ่มเลือกตั๋วความเร็วสูง 150 ใบที่มอบให้กับรถทั้งสีแดงและสีน้ำเงิน เราได้รับ 90 ตั๋วรถสีแดงและ 60 สำหรับรถสีน้ำเงิน ซึ่งต่างจากผลลัพธ์ที่เราคาดไว้ นั่นคือ 100 และ 50. การทดลองควบคุมของเรา (ในกรณีนี้ การเปลี่ยนแหล่งข้อมูลจากระดับชาติเป็นระดับท้องถิ่น) ทำให้เกิดการเปลี่ยนแปลงในผลลัพธ์ หรือตำรวจเมืองของเรามีแนวโน้มเช่นเดียวกับระดับชาติ และเราเพิ่งสังเกตเห็นความบังเอิญหรือไม่ ค่า p จะช่วยให้เราระบุได้

ขั้นตอนที่ 3 กำหนดระดับความอิสระสำหรับการทดสอบของคุณ

องศาความเป็นอิสระเป็นตัววัดปริมาณความแปรปรวนในการศึกษา ซึ่งพิจารณาจากจำนวนหมวดหมู่ที่คุณตรวจสอบ สมการองศาอิสระคือ องศาอิสระ = n-1 โดยที่ n คือจำนวนหมวดหมู่หรือตัวแปรที่วิเคราะห์ในการทดสอบของคุณ

• ตัวอย่าง: การทดลองของเรามีผลลัพธ์สองประเภท: ประเภทหนึ่งสำหรับรถสีแดงและอีกประเภทสำหรับรถสีน้ำเงิน ดังนั้น ในการทดลองของเรา เรามี 2-1 = 1 ระดับความเป็นอิสระ

  ถ้าเราเปรียบเทียบรถสีแดง สีน้ำเงิน และสีเขียว เราจะมี

  ขั้นตอนที่ 2. องศาของเสรีภาพและอื่น ๆ

ขั้นตอนที่ 4 เปรียบเทียบผลลัพธ์ที่คาดหวังกับผลลัพธ์ที่สังเกตได้โดยใช้ไคกำลังสอง

จิกำลังสอง (เขียน x²) เป็นค่าตัวเลขที่วัดความแตกต่างระหว่างค่าที่คาดหวังและค่าที่สังเกตได้จากการทดลอง สมการของไคกำลังสองคือ: NS² = ((o-e)²/จ) โดยที่ o คือค่าที่สังเกตได้ และ e คือค่าที่คาดหวัง บวกผลลัพธ์ของสมการนี้สำหรับผลลัพธ์ที่เป็นไปได้ทั้งหมด (ดูด้านล่าง)

• โปรดทราบว่าสมการนี้ใช้ตัวดำเนินการ (sigma) กล่าวอีกนัยหนึ่ง คุณต้องคำนวณ ((|o-e|-.05)²/e) สำหรับแต่ละผลลัพธ์ที่เป็นไปได้ จากนั้นรวมผลลัพธ์เพื่อให้ได้ค่าไคกำลังสอง ในตัวอย่างของเรา เรามีสองผลลัพธ์ – รถที่ได้รับตั๋วสีแดงหรือสีน้ำเงิน ดังนั้นเราสามารถคำนวณ ((o-e)²/e) สองครั้ง – หนึ่งครั้งสำหรับรถสีแดงและอีกครั้งสำหรับรถสีน้ำเงิน

• ตัวอย่าง: ลองแทนค่าที่คาดหวังและการสังเกตของเราลงในสมการ x² = ((o-e)²/จ). จำไว้ว่า เนื่องจากตัวดำเนินการซิกมา เราต้องคำนวณ ((o-e)²/e) สองครั้ง – หนึ่งครั้งสำหรับรถสีแดงและอีกครั้งสำหรับรถสีน้ำเงิน ขั้นตอนการประมวลผลมีดังนี้:

  • NS² = ((90-100)²/100) + (60-50)²/50)
  • NS² = ((-10)²/100) + (10)²/50)
  • NS² = (100/100) + (100/50) = 1 + 2 = 3.

ขั้นตอนที่ 5. เลือกระดับความสำคัญ

ตอนนี้เรารู้ดีกรีอิสระของชุดทดลองและค่าไคกำลังสองแล้ว มีเพียงสิ่งสุดท้ายที่เราต้องทำก่อนที่เราจะหาค่า p ได้ – เราจำเป็นต้องกำหนดระดับนัยสำคัญ โดยพื้นฐานแล้ว ระดับนัยสำคัญคือการวัดว่าเรามั่นใจในผลลัพธ์ของเรามากเพียงใด – ระดับนัยสำคัญในระดับต่ำสอดคล้องกับความน่าจะเป็นต่ำที่ผลลัพธ์ของการทดสอบเกิดจากโอกาสและในทางกลับกัน ระดับนัยสำคัญเขียนเป็นทศนิยม (เช่น 0.01) ซึ่งสอดคล้องกับเปอร์เซ็นต์โอกาสที่ผลลัพธ์ของการทดสอบเกิดจากโอกาส (ในกรณีนี้คือ 1%)

• ตามแบบแผน นักวิทยาศาสตร์มักจะตั้งค่านัยสำคัญสำหรับการทดลองของพวกเขาที่ 0.05 หรือ 5 เปอร์เซ็นต์ ซึ่งหมายความว่าผลการทดลองที่สอดคล้องกับระดับนัยสำคัญนี้มีโอกาสมากที่สุด 5% ที่จะเกิดขึ้นโดยบังเอิญ กล่าวอีกนัยหนึ่ง มีโอกาส 95% ที่ผลลัพธ์เกิดจากการที่นักวิทยาศาสตร์จัดการตัวแปรทดลอง ไม่ใช่โอกาส สำหรับการทดลองส่วนใหญ่ ความมั่นใจ 95% เกี่ยวกับความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นถือว่าประสบความสำเร็จในการแสดงให้เห็นถึงความสัมพันธ์ระหว่างทั้งสอง
• ตัวอย่าง: สำหรับตัวอย่างรถสีแดงและสีน้ำเงินของเรา ให้ทำตามข้อตกลงทางวิทยาศาสตร์และกำหนดระดับนัยสำคัญของ 0, 05.

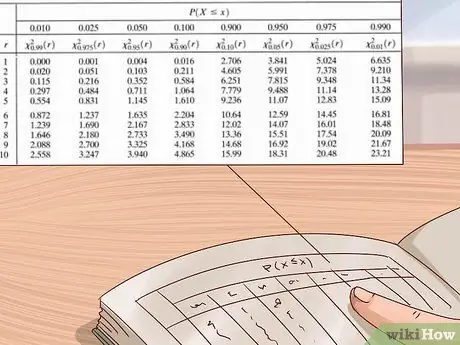
ขั้นตอนที่ 6 ใช้ตารางการแจกแจงไคสแควร์เพื่อประมาณค่า p ของคุณ

นักวิทยาศาสตร์และนักสถิติใช้ตารางค่าขนาดใหญ่เพื่อคำนวณค่า p สำหรับการทดลอง ตารางนี้มักจะเขียนด้วยแกนตั้งทางด้านซ้ายแสดงองศาอิสระและแกนนอนด้านบนแสดงค่า p ใช้ตารางนี้โดยค้นหาองศาอิสระของคุณก่อน จากนั้นจึงอ่านแถวจากซ้ายไปขวาจนกว่าคุณจะพบค่าแรกที่มากกว่าค่าไคกำลังสองของคุณ ดูค่า p ที่ด้านบนสุดของคอลัมน์ – ค่า p ของคุณอยู่ระหว่างค่านี้กับค่าที่มากที่สุดรองลงมา (ค่าที่ถูกต้องจะอยู่ทางซ้ายของค่านั้น)

• ตารางการแจกจ่าย Chi Square มีให้จากแหล่งต่างๆ - สามารถพบได้ทางออนไลน์หรือในตำราวิทยาศาสตร์หรือสถิติ หากคุณไม่มี ให้ใช้ตารางที่แสดงในรูปภาพด้านบนหรือตารางออนไลน์ฟรี เช่น ตารางที่ medcalc.org ให้ไว้ที่นี่

• ตัวอย่าง: ไคกำลังสองของเราคือ 3 ลองใช้ตารางการกระจายไคสแควร์ในภาพด้านบนเพื่อหาค่า p โดยประมาณ เนื่องจากเรารู้ว่าการทดลองของเรามีเพียง

  ขั้นตอนที่ 1. องศาอิสระ เราจะเริ่มจากตารางด้านบน เราไปจากซ้ายไปขวาในแถวนี้จนพบค่าที่สูงกว่า

  ขั้นตอนที่ 3 – ค่าไคกำลังสองของเรา ค่าแรกที่เราพบคือ 3.84 เมื่อมองหาคอลัมน์นี้ เราจะเห็นว่าค่า p ที่สอดคล้องกันคือ 0.05 ซึ่งหมายความว่าค่า p ของเราคือ ระหว่าง 0.05 ถึง 0.1 (ค่า p ที่ใหญ่ที่สุดถัดไปในตาราง)

ขั้นตอนที่ 7 ตัดสินใจว่าจะปฏิเสธหรือปกป้องสมมติฐานว่างของคุณ

เนื่องจากคุณพบค่า p โดยประมาณสำหรับการทดสอบของคุณ คุณจึงสามารถตัดสินใจได้ว่าจะปฏิเสธสมมติฐานว่างของการทดสอบหรือไม่ (เพื่อเป็นการเตือนความจำ นี่คือสมมติฐานที่ว่าตัวแปรทดลองที่คุณจัดการไม่มีผลกับผลลัพธ์ที่คุณสังเกตเห็น) หากค่า p ของคุณต่ำกว่าค่านัยสำคัญ ขอแสดงความยินดีด้วย คุณได้พิสูจน์แล้วว่ามีความเป็นไปได้สูงที่จะมีความสัมพันธ์ระหว่างตัวแปรที่คุณจัดการกับการสังเกตของคุณ หากค่า p ของคุณมากกว่าค่านัยสำคัญ คุณไม่สามารถพูดได้อย่างแน่นอนว่าผลลัพธ์ที่คุณกำลังสังเกตอยู่นั้นเป็นผลมาจากความบังเอิญหรือการปรับเปลี่ยนการทดลองของคุณ

• ตัวอย่าง: ค่า p ของเราอยู่ระหว่าง 0.05 ถึง 0.1 นั่นคือไม่ต่ำกว่า 0.05 เลย น่าเสียดายที่เรา ไม่สามารถปฏิเสธสมมติฐานว่างของเราได้. ซึ่งหมายความว่าเรายังไม่ถึงขีดจำกัดความเชื่อมั่นขั้นต่ำ 95% ที่เราตั้งไว้ เรียกได้ว่าตำรวจในเมืองของเราแจกตั๋วรถสีแดงและสีน้ำเงินในอัตราส่วนที่ค่อนข้างแตกต่างไปจากค่าเฉลี่ยของประเทศ
• กล่าวอีกนัยหนึ่ง มีโอกาส 5-10% ที่การสังเกตของเราไม่ได้เป็นผลมาจากการเปลี่ยนแปลงสถานที่ (การวิเคราะห์เมืองของเราและไม่ใช่ทั้งหมด) แต่เป็นเรื่องบังเอิญ เนื่องจากเรากำลังมองหาความน่าจะเป็นน้อยกว่า 5% เราจึงบอกไม่ได้ว่าเรา มั่นใจ ว่าตำรวจในเมืองของเรามักจะออกตั๋วรถสีแดง – มีความเป็นไปได้เล็กน้อยแต่แตกต่างกันมากทางสถิติที่พวกเขาไม่มีแนวโน้มนี้

เคล็ดลับ

• เครื่องคิดเลขวิทยาศาสตร์จะทำให้การคำนวณง่ายขึ้นมาก คุณยังสามารถค้นหาเครื่องคิดเลขออนไลน์ได้อีกด้วย
• คุณสามารถคำนวณค่า p โดยใช้โปรแกรมคอมพิวเตอร์หลายโปรแกรม รวมถึงซอฟต์แวร์สเปรดชีตที่ใช้กันทั่วไปและซอฟต์แวร์ทางสถิติเฉพาะทางมากขึ้น