3 วิธีในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์อันดับของสเปียร์แมน

2024 ผู้เขียน: Jason Gerald | [email protected]. แก้ไขล่าสุด: 2023-12-16 11:42

ด้วยค่าสัมประสิทธิ์สหสัมพันธ์อันดับของ Spearman เราสามารถระบุได้ว่าตัวแปรสองตัวมีความสัมพันธ์แบบโมโนโทนิกหรือไม่ (นั่นคือ เมื่อจำนวนหนึ่งเพิ่มขึ้น อีกจำนวนหนึ่งจะเพิ่มขึ้นด้วย หรือในทางกลับกัน) ในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์อันดับของ Spearman คุณต้องจัดอันดับและเปรียบเทียบชุดข้อมูลเพื่อค้นหา d²จากนั้นป้อนข้อมูลลงในสูตรสัมประสิทธิ์สหสัมพันธ์อันดับมาตรฐานหรือแบบง่ายของสเปียร์แมน คุณยังสามารถคำนวณสัมประสิทธิ์เหล่านี้ได้โดยใช้สูตร Excel หรือคำสั่ง R

ขั้นตอน

วิธีที่ 1 จาก 3: วิธีด้วยตนเอง

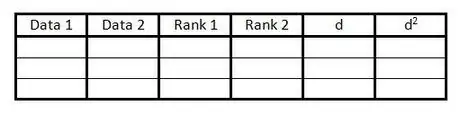
ขั้นตอนที่ 1. สร้างตาราง

ตารางนี้ใช้เพื่อรวมข้อมูลทั้งหมดที่จำเป็นในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์อันดับสเปียร์แมน คุณต้องการตารางแบบนี้:

• สร้าง 6 คอลัมน์พร้อมหัวเรื่องตามตัวอย่าง
• เตรียมแถวว่างให้มากเท่าจำนวนคู่ข้อมูล

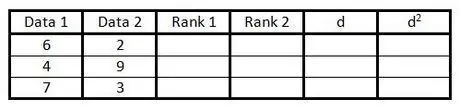
ขั้นตอนที่ 2 กรอกข้อมูลในสองคอลัมน์แรกด้วยคู่ข้อมูล

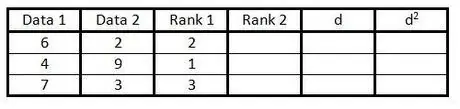
ขั้นตอนที่ 3 ป้อนการจัดอันดับคอลัมน์แรกของกลุ่มข้อมูลในคอลัมน์ที่สามจาก 1 ถึง n (จำนวนข้อมูล)

ให้คะแนน 1 สำหรับค่าต่ำสุด ให้คะแนน 2 สำหรับค่าต่ำสุดถัดไป และอื่นๆ

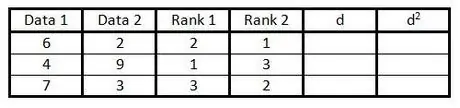
ขั้นตอนที่ 4 ในคอลัมน์ที่สี่ ทำเช่นเดียวกับในขั้นตอนที่ 3 แต่เพื่อจัดอันดับข้อมูลในคอลัมน์ที่สอง

• 

  หากมีข้อมูลสองรายการ (หรือมากกว่า) ที่มีค่าเท่ากัน ให้คำนวณคะแนนเฉลี่ยของข้อมูล แล้วป้อนลงในตารางตามค่าเฉลี่ยนี้

  ในตัวอย่างทางด้านขวา มีค่า 5 สองค่าในการให้คะแนน 2 และ 3 เนื่องจากมีค่า 5 สองค่า ให้หาค่าเฉลี่ยของการให้คะแนน ค่าเฉลี่ยของ 2 และ 3 คือ 2.5 ดังนั้นให้ป้อนค่าการจัดอันดับ 2.5 สำหรับทั้งสองค่า 5

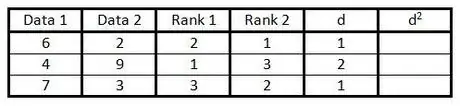
ขั้นตอนที่ 5. ในคอลัมน์ "d" ให้คำนวณความแตกต่างระหว่างตัวเลขสองตัวในคอลัมน์อันดับ

นั่นคือ หากคอลัมน์หนึ่งอยู่ในอันดับที่ 1 และอีกคอลัมน์หนึ่งอยู่ในอันดับที่ 3 ความแตกต่างคือ 2 (เครื่องหมายไม่สำคัญ เพราะขั้นตอนต่อไปคือการยกกำลังสองค่า)

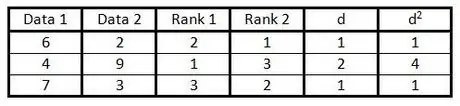
ขั้นตอนที่ 6 ยกกำลังสองแต่ละตัวเลขในคอลัมน์ "d" และเขียนผลลัพธ์ในคอลัมน์ "d²".

ขั้นตอนที่ 7 เพิ่มข้อมูลทั้งหมดในคอลัมน์ d²".

ผลลัพธ์คือ d².

ขั้นตอนที่ 8 เลือกหนึ่งในสูตรต่อไปนี้:

• หากไม่มีการจัดอันดับใดเหมือนกับในขั้นตอนก่อนหน้า ให้ป้อนค่านี้ในสูตรสัมประสิทธิ์สหสัมพันธ์อันดับสเปียร์แมนแบบง่าย

  

  และแทนที่ "n" ด้วยจำนวนคู่ข้อมูลเพื่อให้ได้ผลลัพธ์

  

• หากมีอันดับที่คล้ายกันในขั้นตอนก่อนหน้านี้ ให้ใช้สูตรสัมประสิทธิ์สหสัมพันธ์อันดับสเปียร์มาตรฐาน:

  

ขั้นตอนที่ 9 ตีความผลลัพธ์

ค่าสามารถเปลี่ยนแปลงได้ระหว่าง -1 ถึง 1

• หากค่าใกล้เคียงกับ -1 ความสัมพันธ์จะเป็นลบ
• หากค่าใกล้เคียงกับ 0 จะไม่มีความสัมพันธ์เชิงเส้นตรง
• ถ้าค่าเข้าใกล้ 1 ความสัมพันธ์จะเป็นบวก

วิธีที่ 2 จาก 3: การใช้ Excel

ขั้นตอนที่ 1 สร้างคอลัมน์ใหม่สำหรับข้อมูลพร้อมกับการจัดอันดับ

ตัวอย่างเช่น หากข้อมูลของคุณอยู่ในคอลัมน์ A2:A11 ให้ใช้สูตร "=RANK(A2, A$2:A$11)" และคัดลอกลงไปจนครอบคลุมคอลัมน์และแถวทั้งหมด

ขั้นตอนที่ 2 เปลี่ยนคะแนนเดียวกันตามที่อธิบายไว้ในขั้นตอนที่ 3 และ 4 ของวิธีที่ 1

ขั้นตอนที่ 3 ในเซลล์ใหม่ คำนวณความสัมพันธ์ระหว่างสองคอลัมน์อันดับด้วยสูตร "=CORREL(C2:C11, D2:D11)"

ในตัวอย่างนี้ C และ D หมายถึงคอลัมน์ที่มีการจัดอันดับ เซลล์ใหม่จะเต็มไปด้วยความสัมพันธ์ของอันดับสเปียร์แมน

วิธีที่ 3 จาก 3: การใช้R

ขั้นตอนที่ 1. ติดตั้งโปรแกรม R ก่อน หากคุณยังไม่มี

(ดู

ขั้นตอนที่ 2 บันทึกข้อมูลของคุณในรูปแบบ CSV ใส่ข้อมูลที่คุณต้องการค้นหาความสัมพันธ์ในสองคอลัมน์แรก

เราสามารถทำได้โดยใช้เมนู "บันทึกเป็น"

ขั้นตอนที่ 3 เปิดตัวแก้ไข R

หากคุณกำลังทำงานจากเทอร์มินัล เพียงเรียกใช้ R หากคุณทำงานจากเดสก์ท็อป ให้คลิกไอคอน R

ขั้นตอนที่ 4 พิมพ์คำสั่งต่อไปนี้:

• d <- read.csv("NAME_OF_YOUR_CSV.csv") แล้วกด Enter
• นักแสดง(อันดับ(d[, 1]), อันดับ(d[, 2]))

เคล็ดลับ

ข้อมูลต้องประกอบด้วยอย่างน้อย 5 คู่เพื่อให้สามารถเห็นแนวโน้มได้ (จำนวนข้อมูลคือ 3 คู่ในตัวอย่างเท่านั้นเพื่อทำให้การคำนวณง่ายขึ้น)

คำเตือน

• ค่าสัมประสิทธิ์สหสัมพันธ์อันดับของ Spearman ระบุเฉพาะความแข็งแกร่งของสหสัมพันธ์ที่ข้อมูลเพิ่มขึ้นหรือลดลงอย่างสม่ำเสมอ หากมีแนวโน้มอื่นในข้อมูล สหสัมพันธ์อันดับของ Spearman ไม่ จะให้การแสดงที่ถูกต้อง
• สูตรนี้ใช้สมมติฐานว่าไม่มีการให้คะแนนเท่ากัน เมื่อมีอันดับเดียวกับในตัวอย่าง เราควรใช้คำจำกัดความนี้: สัมประสิทธิ์สหสัมพันธ์ของโมเมนต์การคูณด้วยอันดับ