วิธีการคำนวณการลอยตัว: 12 ขั้นตอน (พร้อมรูปภาพ)

2024 ผู้เขียน: Jason Gerald | [email protected]. แก้ไขล่าสุด: 2024-01-19 22:14

แรงลอยตัวเป็นแรงที่อยู่ตรงข้ามกับแรงโน้มถ่วง ซึ่งส่งผลต่อวัตถุทั้งหมดที่จมอยู่ในของเหลว เมื่อวางวัตถุลงในของเหลว มวลของวัตถุจะกดทับของเหลว (ของเหลวหรือก๊าซ) ในขณะที่แรงลอยตัวผลักวัตถุต้านแรงโน้มถ่วง โดยทั่วไป แรงลอยตัวนี้สามารถคำนวณได้โดยสมการ NS_NS = ว_NS × × ก, กับ F_NS เป็นแรงลอยตัว V_NS คือปริมาตรของวัตถุที่จมอยู่ใต้น้ำ คือ ความหนาแน่นของของไหล และ g คือแรงโน้มถ่วง หากต้องการเรียนรู้วิธีกำหนดความลอยตัวของวัตถุ โปรดดูขั้นตอนที่ 1 ด้านล่างเพื่อเริ่มต้น

ขั้นตอน

วิธีที่ 1 จาก 2: การใช้สมการการลอยตัว

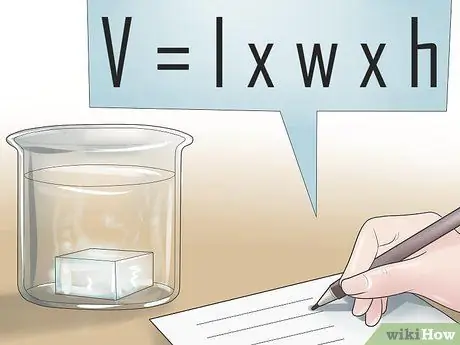
ขั้นตอนที่ 1 ค้นหาปริมาตรของส่วนที่จมอยู่ใต้น้ำของวัตถุ

แรงลอยตัวที่กระทำต่อวัตถุนั้นเป็นสัดส่วนกับปริมาตรของวัตถุที่จมอยู่ใต้น้ำ กล่าวอีกนัยหนึ่ง ยิ่งส่วนที่เป็นของแข็งที่จมอยู่ใต้น้ำของวัตถุยิ่งใหญ่เท่าใด แรงลอยตัวที่กระทำต่อวัตถุก็จะยิ่งมากขึ้นเท่านั้น ซึ่งหมายความว่าวัตถุที่จมอยู่ในของเหลวจะมีแรงลอยตัวที่ดันวัตถุขึ้น ในการเริ่มต้นคำนวณแรงลอยตัวที่กระทำต่อวัตถุ ขั้นตอนแรกของคุณมักจะกำหนดปริมาตรของวัตถุที่จมอยู่ในของเหลว สำหรับสมการการลอยตัว ค่านี้ควรเป็นเมตร³.

• สำหรับวัตถุที่จมอยู่ในของเหลวอย่างสมบูรณ์ ปริมาตรที่จมอยู่ใต้น้ำจะเท่ากับปริมาตรของวัตถุเอง สำหรับวัตถุที่ลอยอยู่เหนือพื้นผิวของของไหล จะคำนวณเฉพาะปริมาตรที่อยู่ใต้พื้นผิวเท่านั้น
• ตัวอย่างเช่น สมมติว่าเราต้องการหาแรงลอยตัวที่กระทำต่อลูกยางที่ลอยอยู่บนน้ำ หากลูกยางเป็นทรงกลมสมบูรณ์ที่มีเส้นผ่านศูนย์กลาง 1 ม. และลอยโดยครึ่งหนึ่งจมอยู่ใต้น้ำ เราจะสามารถหาปริมาตรของส่วนที่จมอยู่ใต้น้ำได้โดยการหาปริมาตรรวมของทรงกลมแล้วหารด้วยสอง เนื่องจากปริมาตรของทรงกลมคือ (4/3) (รัศมี)³, เรารู้ว่าปริมาตรของทรงกลมของเราคือ (4/3)π(0, 5)³ = 0.524 เมตร³. 0, 524/2 = 0.262 เมตร³ จม.

ขั้นตอนที่ 2 ค้นหาความหนาแน่นของของเหลวของคุณ

ขั้นตอนต่อไปในกระบวนการหาแรงลอยตัวคือการกำหนดความหนาแน่น (เป็นกิโลกรัม/เมตร³) ของของไหลที่วัตถุแช่อยู่ ความหนาแน่นคือการวัดมวลของวัตถุหรือสารที่สัมพันธ์กับปริมาตรของมัน ถ้าให้วัตถุสองชิ้นที่มีปริมาตรเท่ากัน วัตถุที่มีความหนาแน่นมากกว่าจะมีมวลมากกว่า ตามกฎ ยิ่งความหนาแน่นของของไหลที่วัตถุจมอยู่ใต้น้ำมากเท่าใด แรงลอยตัวก็จะยิ่งมากขึ้นเท่านั้น สำหรับของเหลว วิธีที่ง่ายที่สุดในการระบุความหนาแน่นคือการค้นหาในวัสดุอ้างอิง

• ในตัวอย่างของเรา ลูกบอลของเราลอยอยู่ในน้ำ เมื่อพิจารณาจากแหล่งข้อมูลทางวิชาการแล้ว เราจะพบว่าน้ำมีความหนาแน่นประมาณ 1,000 กิโลกรัม/เมตร³.
• ความหนาแน่นของของไหลอื่นๆ ที่ใช้กันอย่างแพร่หลายมีระบุไว้ในแหล่งทางวิศวกรรม รายการหนึ่งสามารถพบได้ที่นี่

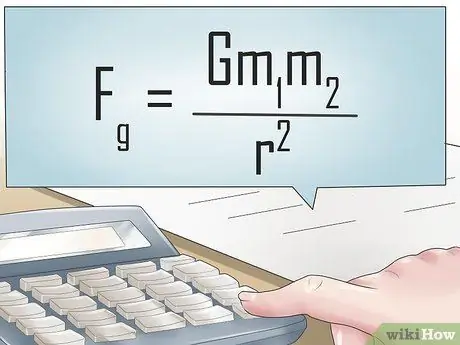
ขั้นตอนที่ 3 ค้นหาแรงโน้มถ่วง (หรือแรงลงอื่นๆ)

ไม่ว่าวัตถุจะจมหรือลอยอยู่ในของเหลว วัตถุนั้นก็มีแรงโน้มถ่วงเสมอ ในโลกแห่งความเป็นจริง ค่าคงที่แรงลงเท่ากับ 9.81 นิวตัน/กิโลกรัม. อย่างไรก็ตาม ในสถานการณ์ที่แรงอื่นๆ เช่น แรงเหวี่ยงหนีศูนย์กลาง กระทำต่อของไหลและวัตถุที่จมอยู่ในนั้น แรงนี้จะต้องนำมาพิจารณาด้วยเพื่อกำหนดแรงลงสุทธิสำหรับทั้งระบบ

• ในตัวอย่างของเรา เรากำลังทำงานกับระบบสถิตย์ธรรมดา ดังนั้นเราสามารถสรุปได้ว่าแรงลงที่กระทำต่อของไหลและวัตถุเพียงอย่างเดียวคือแรงโน้มถ่วงทั่วไป - 9.81 นิวตัน/กิโลกรัม.
• อย่างไรก็ตาม จะเกิดอะไรขึ้นถ้าลูกบอลของเราซึ่งลอยอยู่ในถังน้ำ ถูกเหวี่ยงเป็นวงกลมในแนวนอนด้วยความเร็วสูง ในกรณีนี้ สมมติว่าถังเหวี่ยงเร็วพอที่น้ำและลูกบอลไม่หก แรงที่ลดลงในสถานการณ์นี้จะมาจากแรงเหวี่ยงหนีศูนย์กลางที่เกิดจากการแกว่งของถัง ไม่ใช่จากแรงโน้มถ่วงของโลก

ขั้นตอนที่ 4 คูณปริมาตร x ความหนาแน่น x แรงโน้มถ่วง

หากคุณมีค่าปริมาตรของวัตถุของคุณ (เป็นเมตร³) ความหนาแน่นของของเหลวของคุณ (เป็นกิโลกรัม/เมตร³) และแรงโน้มถ่วง (แรงที่ลดลงในระบบของคุณ) ดังนั้น การค้นหาทุ่นลอยน้ำจึงเป็นเรื่องง่ายมาก เพียงคูณค่าทั้งสามนี้เพื่อหาแรงลอยตัวในหน่วยนิวตัน

มาแก้ปัญหาตัวอย่างของเราโดยแทนค่าของเราลงในสมการ F_NS = ว_NS × × ก. NS_NS = 0.262 เมตร³ × 1,000 กิโลกรัม/เมตร³ × 9.81 นิวตัน/กิโลกรัม = 2,570 นิวตัน.

ขั้นตอนที่ 5. ดูว่าวัตถุของคุณลอยโดยการเปรียบเทียบการลอยตัวกับแรงโน้มถ่วง

เมื่อใช้สมการการลอยตัว การหาแรงที่ผลักวัตถุขึ้นและออกจากของเหลวนั้นเป็นเรื่องง่าย อย่างไรก็ตาม ด้วยความพยายามพิเศษเพียงเล็กน้อย ก็สามารถระบุได้เช่นกันว่าวัตถุจะลอยหรือจม เพียงแค่หาแรงลอยตัวของวัตถุทั้งหมด (กล่าวคือ ใช้ปริมาตรทั้งหมดแทนค่า V_NS) แล้วหาแรงโน้มถ่วงที่ผลักลงมาด้วยสมการ G = (มวลของวัตถุ)(9.81 เมตร/วินาที)²). ถ้าแรงลอยตัวมากกว่าแรงโน้มถ่วง วัตถุจะลอย ในทางกลับกัน ถ้าแรงโน้มถ่วงมากกว่าแรงลอยตัว วัตถุก็จะจมลง ถ้าขนาดเท่ากัน ถือว่าวัตถุลอย

• ตัวอย่างเช่น สมมติว่าเราต้องการทราบว่าถังไม้ทรงกระบอกที่มีมวล 20 กิโลกรัมและมีเส้นผ่านศูนย์กลาง 0.75 ม. และสูง 1.25 ม. จะลอยอยู่ในน้ำหรือไม่ ปัญหานี้จะใช้หลายขั้นตอน:

  • เราสามารถหาปริมาตรได้ด้วยสูตรหาปริมาตรของทรงกระบอก V = (รัศมี)²(สูง). วี = (0, 375)²(1, 25) = 0.55 เมตร³.
  • ต่อไป สมมติว่าแรงโน้มถ่วงปกติและความหนาแน่นปกติ เราจะสามารถหาแรงลอยตัวของถัง 0.55 เมตร³ × 1,000 กิโลกรัม/เมตร³ × 9.81 นิวตัน/กิโลกรัม = 5,395, 5 นิวตัน.
  • ตอนนี้ เราต้องหาแรงโน้มถ่วงของลำกล้องปืน G = (20 กก.)(9.81 เมตร/วินาที²) = 196.2 นิวตัน. แรงนี้น้อยกว่าแรงลอยตัว ดังนั้นลำกล้องจะลอย

ขั้นตอนที่ 6 ใช้แนวทางเดียวกันหากของเหลวของคุณเป็นก๊าซ

เมื่อทำงานกับปัญหาการลอยตัว อย่าลืมว่าของเหลวที่วัตถุจมอยู่ใต้น้ำไม่จำเป็นต้องเป็นของเหลว ก๊าซก็เป็นของเหลวเช่นกัน และแม้ว่าก๊าซจะมีความหนาแน่นต่ำมากเมื่อเทียบกับสารอื่นๆ แต่ก็ยังสามารถรองรับมวลของวัตถุที่ลอยอยู่ในก๊าซได้ บอลลูนฮีเลียมธรรมดาเป็นข้อพิสูจน์ เนื่องจากก๊าซในบอลลูนมีความหนาแน่นน้อยกว่าของเหลวโดยรอบ (อากาศแวดล้อม) บอลลูนจึงลอยได้!

วิธีที่ 2 จาก 2: ทำการทดสอบการลอยตัวอย่างง่าย

ขั้นตอนที่ 1. วางชามหรือถ้วยเล็กไว้ในชามใบใหญ่

ของใช้ในครัวเรือนบางรายการ เป็นเรื่องง่ายที่จะเห็นหลักการลอยตัวในการทดลอง! ในการทดลองง่ายๆ นี้ เราจะแสดงให้เห็นว่าวัตถุที่จมอยู่ใต้น้ำประสบกับแรงลอยตัว เพราะมันจะเปลี่ยนปริมาตรของของไหลเท่ากับปริมาตรของวัตถุที่จมอยู่ใต้น้ำ เมื่อเราทำเช่นนี้ เราจะสาธิตวิธีปฏิบัติในการค้นหาแรงลอยตัวของวัตถุด้วยการทดลองนี้ด้วย ในการเริ่มต้น ให้วางภาชนะเปิดขนาดเล็ก เช่น ชามหรือถ้วย ไว้ในภาชนะที่ใหญ่กว่า เช่น ชามหรือถังขนาดใหญ่

ขั้นตอนที่ 2 เติมภาชนะขนาดเล็กให้เต็ม

ถัดไป เติมน้ำในภาชนะด้านในที่มีขนาดเล็กกว่า คุณต้องการให้น้ำสูงเท่าภาชนะโดยไม่หก ระวังที่นี่! หากคุณทำน้ำหก ให้ล้างภาชนะที่ใหญ่กว่าก่อนลองอีกครั้ง

• สำหรับวัตถุประสงค์ของการทดลองนี้ จะถือว่าน้ำมีความหนาแน่นทั่วไปอยู่ที่ 1,000 กิโลกรัม/เมตร³. เว้นแต่ว่าคุณกำลังใช้น้ำทะเลหรือของเหลวที่แตกต่างกันโดยสิ้นเชิง น้ำส่วนใหญ่มีความหนาแน่นเกือบเท่ากันกับค่าอ้างอิงนี้ ดังนั้นความแตกต่างเล็กน้อยจะไม่เปลี่ยนแปลงผลลัพธ์ของเรา
• หากคุณมียาหยอดตา สิ่งนี้มีประโยชน์มากสำหรับการเพิ่มระดับน้ำในภาชนะขนาดเล็ก

ขั้นตอนที่ 3 จุ่มวัตถุขนาดเล็กลงไป

ต่อไป ให้มองหาวัตถุขนาดเล็กที่จะพอดีกับภาชนะขนาดเล็กและจะไม่ได้รับความเสียหายจากน้ำ ค้นหามวลของวัตถุนี้เป็นกิโลกรัม (คุณอาจต้องการใช้มาตราส่วนหรือเครื่องชั่งที่นำกรัมมาแปลงเป็นกิโลกรัม) จากนั้นจุ่มวัตถุลงในน้ำช้าๆ แต่แน่นอน โดยไม่ให้นิ้วเปียกจนกว่าจะเริ่มลอยหรือคุณสามารถจับไว้เล็กน้อยแล้วปล่อยออก คุณจะสังเกตเห็นว่าน้ำบางส่วนในภาชนะขนาดเล็กจะหกลงในภาชนะด้านนอก

สำหรับจุดประสงค์ของตัวอย่างของเรา สมมติว่าเราจุ่มรถของเล่นที่มีมวล 0.05 กิโลกรัมลงในภาชนะขนาดเล็ก เราไม่จำเป็นต้องรู้ปริมาตรของรถคันนี้เพื่อคำนวณการลอยตัว เพราะเราจะเห็นกันในขั้นตอนต่อไป

ขั้นตอนที่ 4. รวบรวมและนับน้ำที่หก

เมื่อคุณจุ่มวัตถุลงในน้ำ มันจะแทนที่น้ำบางส่วน มิฉะนั้นจะไม่มีที่สำหรับวางวัตถุนั้นลงในน้ำ เมื่อวัตถุผลักน้ำออก น้ำจะดันกลับ ทำให้เกิดแรงลอยตัว นำน้ำที่หกออกจากภาชนะขนาดเล็กแล้วเทลงในถ้วยตวงขนาดเล็ก ปริมาตรของน้ำในถ้วยตวงเท่ากับปริมาตรของวัตถุที่จมอยู่ใต้น้ำ

กล่าวอีกนัยหนึ่ง ถ้าวัตถุของคุณลอย ปริมาตรของน้ำที่ไหลออกมาจะเท่ากับปริมาตรของวัตถุที่จมอยู่ใต้ผิวน้ำ หากวัตถุของคุณจม ปริมาตรของน้ำที่ไหลออกมาจะเท่ากับปริมาตรทั้งหมดของวัตถุ

ขั้นตอนที่ 5. คำนวณมวลของน้ำที่หก

เนื่องจากคุณทราบความหนาแน่นของน้ำและคุณสามารถวัดปริมาตรของน้ำที่หกในถ้วยตวงได้ คุณจึงสามารถหามวลของน้ำได้ แค่เปลี่ยนระดับเสียงเป็นเมตร³ (ตัวช่วยแปลงออนไลน์แบบนี้ช่วยได้) และคูณด้วยความหนาแน่นของน้ำ (1,000 กิโลกรัม/เมตร)³).

ในตัวอย่างของเรา สมมติว่ารถของเล่นของเราจมลงในภาชนะขนาดเล็กและเคลื่อนตัวได้ประมาณสองช้อนโต๊ะ (0.0003 เมตร³). ในการหามวลของน้ำ เราจะคูณมันด้วยความหนาแน่น: 1,000 กิโลกรัม/เมตร³ × 0.0003 เมตร³ = 0.03 กิโลกรัม.

ขั้นตอนที่ 6 เปรียบเทียบมวลของน้ำที่หกกับมวลของวัตถุ

เมื่อคุณทราบมวลของวัตถุที่คุณกำลังจมอยู่ในน้ำและมวลของน้ำที่หกแล้ว ให้เปรียบเทียบกันเพื่อดูว่ามวลใดมีขนาดใหญ่กว่ากัน ถ้ามวลของวัตถุที่จมอยู่ในภาชนะขนาดเล็กมีค่ามากกว่าน้ำที่หก วัตถุนั้นก็จะจมลง ในทางกลับกัน ถ้ามวลของน้ำที่หกมากกว่า วัตถุก็จะลอย นี่คือหลักการลอยตัวในการทดลอง - เพื่อให้วัตถุลอยได้ จะต้องแทนที่ปริมาณน้ำที่มีมวลมากกว่ามวลของตัววัตถุเอง

• ดังนั้นวัตถุที่มีมวลน้อยแต่มีปริมาตรมากจึงเป็นประเภทของวัตถุที่ลอยได้ง่ายที่สุด คุณสมบัตินี้หมายความว่าวัตถุกลวงลอยได้ง่ายมาก ลองนึกภาพเรือแคนู - เรือแคนูลอยได้ดีเพราะเป็นโพรง จึงสามารถเคลื่อนย้ายน้ำได้มากโดยไม่ต้องมีมวลมาก หากเรือแคนูไม่กลวง (แข็ง) เรือแคนูก็จะลอยได้ไม่ถูกต้อง
• ในตัวอย่างของเรา รถมีมวลมากกว่า (0.05 กิโลกรัม) มากกว่าน้ำที่หก (0.03 กิโลกรัม) สิ่งนี้สอดคล้องกับสิ่งที่เราสังเกตเห็น: รถจม